- Sistemas TC y TD
- Señales TC y TD
- SLIT TC
- SLIT TD
- Fourier TC
- Fourier TD
Selecciona un tema de arriba.
Primero debes seleccionar un tema de arriba.
Señales en TC y en TD:
En los ejercicios propuestos de esta sección el estudiante será capaz de identificar y manipular las señales tanto en tiempo continuo como en discreto. Podrá representar señales mediante funciones matemáticas, identificar su comportamiento y presentar la representación gráfica de ellas.
Selecciona la dificultad en las caritas de la izquierda.
Señales en TC y en TD nivel principiante:
- Defina una función sgn(t), que calcule la señal signum sgn(t), Ecuación 2.10, cuyo parámetro de entrada sea un vector de tiempo t. Utilice la función us(t) previamente generada. Con la función definida, grafique la señal en el intervalo  − 3 ≤ t ≤ 3.
- Defina una función rs(t), que calcule la señal rampa r(t), Ecuación 2.9, cuyo parámetro de entrada sea un vector de tiempo t. Con la función definida, grafique la señal en el intervalo  − 1 ≤ t ≤ 5.
- Defina una función tri(t), Ecuación 2.12, que calcule la señal triángulo tri(t), cuyo parámetro de entrada sea un vector de tiempo t. Utilice la función rs(t) generada en ejercicio anterior. Con la función definida, grafique la señal en el intervalo  − 1 ≤ t ≤ 1.
- Defina una función rd(n) que evalúe la secuencia rampa ramp[n], Ecuación 2.19, cuyo parámetro de entrada sea el vector de tiempo discreto n. Grafique la señal rd(n) en el intervalo  − 1 ≤ n ≤ 10.
Señales en TC y en TD nivel intermedio:
-
Considere la señal exponencial general, Ecuación 2.22 y defina una función expd(n,C,α), cuyos parámetros sean el vector n, la amplitud C y el valor de α. Grafique las tres señales exponenciales reales con C = 1 y α = 2, α = 0.5, α = 1, en el intervalo de  − 2 ≤ n ≤ 6. Utilice la función subplot para graficar las tres señales.
(2.22) x[n] = Cαn
- Con la función expd(n,C,α), previamente definida, y considerando y , y , y . Utilice la función subplot para graficar las tres señales exponenciales complejas en el intervalo de  − 5 ≤ n ≤ 10.. Ya que las señales son complejas, es necesario graficar la parte real y la parte imaginaria, o bien la magnitud y la fase de las señales.
-
Con la función expd(n,C,α), previamente definida, considere
y ,
,y
. Utilice la función subplot para graficar las tres señales exponenciales complejas en el intervalo de  − 5 ≤ n ≤ 10. Ya que las señales son complejas, es necesario graficar la parte real y la parte imaginaria, o bien la magnitud y la fase de las señales.
Señales en TC y en TD nivel avanzado:
-
Utilizando las funciones de las señales u(t), r(t), previamente generadas, obtenga las gráficas de las siguientes señales:
-
en donde corresponde al ejercicio anterior. -
en donde y corresponden a los 2 ejercicios anteriores.
-
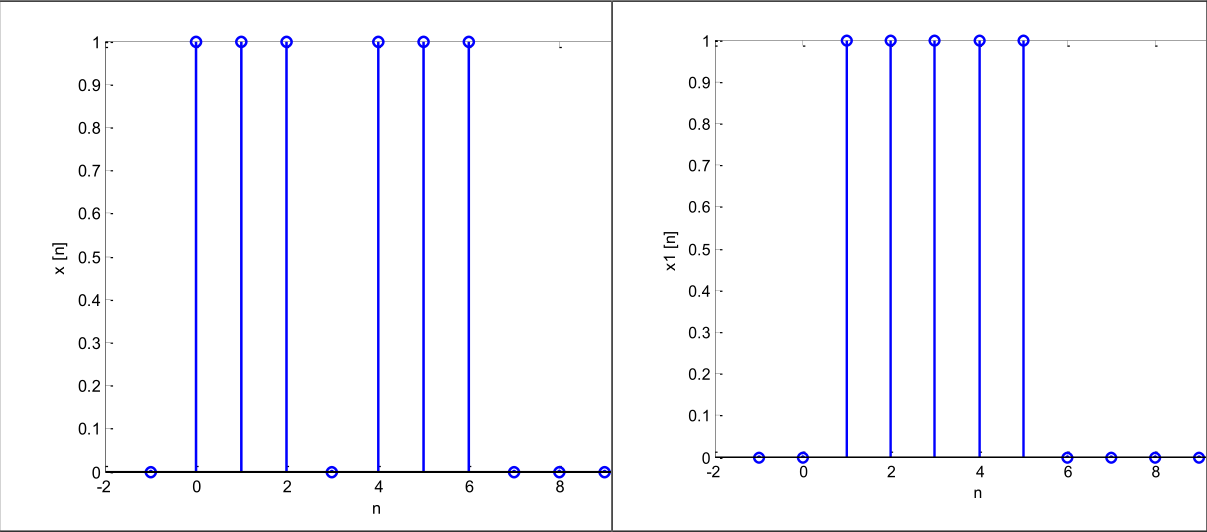
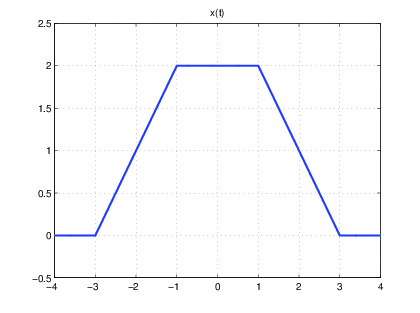
Obtenga una nueva señal x1(t) = x(t − 3), considerando ahora la señal x(t) de la figura. Realice las siguientes transformaciones en x1(t) y grafique las correspondientes señales:
-
Sistemas en TC y TD::
En los ejercicios propuestos de esta sección el estudiante será capaz de identificar los sistemas continuos y discretos. También podrá realizar la clasificación básica referente a la linealidad e invariabilidad en el tiempo.
Selecciona la dificultad en las caritas de la izquierda.
Sistemas en TC y TD: nivel principiante:
1. Indique si el siguiente sistema es:
a) BIBO–estable
b) Causal
c) Invariable en el tiempo
d) Lineal
| y[n] | ‚ÄÖ=‚ÄÖ | H{x[n]} |
| ‚ÄÖ=‚ÄÖ | 2x[n]‚ÄÖ+‚ÄÖx[n‚ÄÖ‚àí‚ÄÖ1] |
2. Indique si el siguiente sistema es:
a) BIBO–estable
b) Causal
c) Invariable en el tiempo
d) Lineal
| y[n] | ‚ÄÖ=‚ÄÖ | H{x[n]} |
| ‚ÄÖ=‚ÄÖ | maÃÅximo(x[n‚ÄÖ‚àí‚ÄÖ1],‚ÄÖ¬Ýx[n],‚ÄÖ¬Ýx[n‚ÄÖ+‚ÄÖ1]);¬Ýa‚Äւ⧂ÄÖn‚Äւ⧂ÄÖb |
Sistemas en TC y TD: nivel intermedio:
a) Invariante en n
b) Lineal
Sistemas en TC y TD: nivel avanzado:
Proponga un sistema lineal en donde al aplicar el principio de linealidad se reduzca el tiempo de ejecución del mismo.
Sistemas Lineales Invariantes en el Tiempo en TC:
En los ejercicios propuestos de esta sección el estudiante podrá identificar y obtener la Respuesta de entrada cero (libre) y respuesta de estado cero (forzada), así como la respuesta transitoria y la respuesta permanente. Reafirmará los conceptos de función de transferencia y diagrama de polos y ceros. Podrá realiza el análisis y la solución tanto de forma analítica como simulada.
Selecciona la dificultad en las caritas de la izquierda.
Sistemas Lineales Invariantes en el Tiempo en TC nivel principiante:
-
Considere el sistema de primer orden indicado, la entrada es x(t)‚ÄÖ=‚ÄÖe‚ÄÖ‚àí‚ÄÖ2tu(t), determine y grafique las respuestas para la salida y(t). (dy(t))/(dt)‚ÄÖ+‚ÄÖ(2)/(5)y(t)‚ÄÖ=‚ÄÖx(t)
- de entrada cero
- de estado cero y al pulso
- total
- transitoria
- permanente
- total, transitoria y permanente para el caso cuando y(0‚ÄÖ‚àí‚ÄÖ)‚ÄÖ=‚ÄÖ0.5
- Repita el problema 3.1 si ahora x(t)‚ÄÖ=‚ÄÖe‚ÄÖ‚àí‚ÄÖ(2t)/(5)u(t).
- Repita el problema 3.1 si ahora x(t)‚ÄÖ=‚ÄÖcos(‚ÄÖ‚àí‚ÄÖ2t)u(t).
-
Verifique los resultados de los problemas 3.1, 3.2 y 3.3 con MATLAB.
- Utilice la función dsolve() similar al ejemplo 3.4.
- Utilice la función lsim(b,a,x,t) para determinar la respuesta del sistema a la entrada x con condiciones iniciales nulas. b y a son vectores que definen al sistema.
- Utilice la función impulse(b,a,t) para determinar la respuesta al impulso del sistema
-
Grafique las respuestas obtenidas en b) y c) con
plot(t,lsim(b,a,x,t)) y plot(t,impulse(b,a,x,t)).
Sistemas Lineales Invariantes en el Tiempo en TC nivel intermedio:
-
Considere el sistema de segundo orden indicado. La entrada es un escalón x(t) = 10u(t) y las condiciones iniciales son nulas. Determine y grafique la respuesta total y(t) para los siguientes casos: a2(d2y(t))/(dt2) + a1(dy(t))/(dt) + a0y(t) = b0x(t)
- ¬Ýa2‚ÄÖ=‚ÄÖ1, ¬Ýa1‚ÄÖ=‚ÄÖ1 y ¬Ýa0‚ÄÖ=‚ÄÖ1.
- ¬Ýa2‚ÄÖ=‚ÄÖ1‚ÄÖ‚ÅÑ‚ÄÖ10, ¬Ýa1‚ÄÖ=‚ÄÖ1 y ¬Ýa0‚ÄÖ=‚ÄÖ10‚ÄÖ‚ÅÑ‚ÄÖ9.
- ¬Ýa2‚ÄÖ=‚ÄÖ1‚ÄÖ‚ÅÑ‚ÄÖ10, ¬Ýa1‚ÄÖ=‚ÄÖ2 y ¬Ýa0‚ÄÖ=‚ÄÖ1‚ÄÖ‚ÅÑ‚ÄÖ10.
-
Repita el problema 3.5 con MATLAB. Utilice las funciones del problema 3.4 para verificar sus respuestas. También son de utilidad las siguientes funciones simbólicas: int(f) evalúa la integral de la función f, diff(f) realiza la diferencial de la función f, roots(a) determina las raíces del vector a.En cualquier caso, vea los detalles con help, por ejemplo help int, etc.
-
Para el sistema en tiempo continuo, modelado por la ecuación diferencial(d2y(t))/(dt2) + 4(dy(t))/(dt) + 6y(t) = x(t)En donde y(t) representa la salida y x(t) la entrada. Determine la respuesta del sistema al impulso y a una entrada escalón. Considere y(0 − ) = 1 y (dy)/(dt)||t = 0 −  = 0.
- Verifique el resultado del problema 3.7 con MATLAB.
Sistemas Lineales Invariantes en el Tiempo en TC nivel avanzado:
-
Si x(t) = ektu(t) y h(t) = estu(t), es la entrada a un sistema de primer orden y la respuesta al impulso del sistema, respectivamente, determine la respuesta de estado cero yzs(t) = x(t)∗h(t) mediante la integral de convolución en forma analítica, gráfica y con MATLAB haciendo uso de la función conv(), para los siguientes casos:
- k‚ÄÖ=‚ÄÖs‚ÄÖ=‚ÄÖ‚ÄÖ‚àí‚ÄÖ2
- k‚ÄÖ=‚ÄÖ‚ÄÖ‚àí‚ÄÖ2 y s‚ÄÖ=‚ÄÖ‚ÄÖ‚àí‚ÄÖ1
-
Determine la convolución w(t) = x1(t)∗x2(t) de las siguientes señales
-
x1(t)‚ÄÖ=‚ÄÖ2r(t‚ÄÖ‚àí‚ÄÖ1)‚ÄÖ‚àí‚ÄÖ2r(t‚ÄÖ‚àí‚ÄÖ3)‚ÄÖ‚àí‚ÄÖ4u(t‚ÄÖ‚àí‚ÄÖ3)
x2(t‚ÄÖ‚àí‚ÄÖ1)‚ÄÖ=‚ÄÖ‚ÄÖ‚àí‚ÄÖ2u(t)‚ÄÖ+‚ÄÖ2u(t‚ÄÖ‚àí‚ÄÖ3) -
x1(t)‚ÄÖ=‚ÄÖ2r(t‚ÄÖ‚àí‚ÄÖ1)‚ÄÖ‚àí‚ÄÖ2r(t‚ÄÖ‚àí‚ÄÖ3)‚ÄÖ‚àí‚ÄÖ4u(t‚ÄÖ‚àí‚ÄÖ3)
x2(t)‚ÄÖ=‚ÄÖ‚ÄÖ‚àí‚ÄÖ2u(t‚ÄÖ‚àí‚ÄÖ2)‚ÄÖ+‚ÄÖ2u(t‚ÄÖ‚àí‚ÄÖ4)
-
x1(t)‚ÄÖ=‚ÄÖ2r(t‚ÄÖ‚àí‚ÄÖ1)‚ÄÖ‚àí‚ÄÖ2r(t‚ÄÖ‚àí‚ÄÖ3)‚ÄÖ‚àí‚ÄÖ4u(t‚ÄÖ‚àí‚ÄÖ3)
-
La propiedad de convolución del impulso unitario con una señal, está dada por x(t) = x(t)∗δ(t)Aplique esta propiedad para determinar la convolución de las siguientes señales: w(t)∗x(t) y w(t)∗z(t). En dondex(t) = 1.5δ(t + 1.5) + 1.5δ(t − 1.5)z(t) = 2δ(t − 0.5) + 4δ(t − 1)w(t) = ⎧⎨⎩ t 0 ≤ t < 2     0  otro valor 
-
Determine la convolución de las siguientes señales: x1(t)∗x2(t), x1(t ⁄ 4)∗x2(t), x1(t)∗x1(t) y x2(t)∗x2(t). En dondex1(t) = u(t − 1.5) − u(t − 2.5)x2(t) = u(t − 2.5) − u(t − 5.5)
Sistemas lineales e invariantes en el tiempo en TD:
En los ejercicios propuestos de esta sección el estudiante podrá identificar y obtener la Respuesta de entrada cero (libre) y respuesta de estado cero (forzada), así como la respuesta transitoria y la respuesta permanente. Reafirmará los conceptos de función de transferencia y diagrama de polos y ceros. Podrá realiza el análisis y la solución tanto de forma analítica como simulada.
Selecciona la dificultad en las caritas de la izquierda.
Sistemas lineales e invariantes en el tiempo en TD nivel principiante:
-
Si la respuesta al impulso es
- Obtenga H(z) y diga si es o no estable el sistema.
- Determine el diagrama de bloques del sistema.
- Obtenga los primeros 5 valores de h[n] mediante recursividad.
- Obtenga la respuesta al escalón mediante convolución.
-
Si la respuesta al impulso es
- Obtenga H(z) y diga si es o no estable el sistema.
- Determine el diagrama de bloques del sistema.
- Obtenga los primeros 5 valores de h[n] mediante recursividad.
- Obtenga la respuesta al escalón mediante convolución.
-
Si la respuesta al impulso es
- Obtenga H(z) y diga si es o no estable el sistema.
- Determine el diagrama de bloques del sistema.
- Obtenga los primeros 5 valores de h[n] mediante recursividad.
- Obtenga la respuesta al escalón mediante convolución.
-
Si la respuesta al impulso es
- Obtenga H(z) y diga si es o no estable el sistema.
- Determine el diagrama de bloques del sistema.
- Obtenga los primeros 5 valores de h[n] mediante recursividad.
- Obtenga la respuesta al escalón mediante convolución.
-
Si la respuesta al impulso es
- Obtenga
- Obtenga H(z) y diga si es o no estable el sistema.
- Determine el diagrama de bloques del sistema.
- Obtenga los primeros 5 valores de h[n] mediante recursividad.
- Obtenga la respuesta al escalón mediante convolución.
-
Si la respuesta al impulso es
- Obtenga H(z) y diga si es o no estable el sistema.
- Determine el diagrama de bloques del sistema.
- Obtenga los primeros 5 valores de h[n] mediante recursividad.
- Obtenga la respuesta al escalón mediante convolución.
-
Si la respuesta al impulso es
- Obtenga H(z) y diga si es o no estable el sistema.
- Determine el diagrama de bloques del sistema.
- Obtenga los primeros 5 valores de h[n] mediante recursividad.
- Obtenga la respuesta al escalón mediante convolución.
-
Si la respuesta al impulso es
- Obtenga H(z) y diga si es o no estable el sistema.
- Determine el diagrama de bloques del sistema.
- Obtenga los primeros 5 valores de h[n] mediante recursividad.
- Obtenga la respuesta al escalón mediante convolución.
-
Si la respuesta al impulso es
- Obtenga H(z) y diga si es o no estable el sistema.
- Determine el diagrama de bloques del sistema.
- Obtenga los primeros 5 valores de h[n] mediante recursividad.
- Obtenga la respuesta al escalón mediante convolución.
-
La función de transferencia de un sistema de 2○ orden es
- Obtenga la expresión de la ecuación en diferencias del sistema.
- Determine la respuesta al impulso h[n] mediante recursividad para los primeros 5 valores.
- Determine la respuesta al impulso h[n] a partir de la función de transferencia.
- Determine el diagrama de polos y ceros e identifique si el sistema es o no estable.
-
La figura muestra la respuesta al impulso de un sistema.
- Identifique y presente la expresión de la respuesta al impulso de la figura.
-
Obtenga la respuesta del sistema, si la entrada es:
- Obtenga mediante TZ la respuesta a una entrada escalón.
- Obtenga la convolución de las señales
Sistemas lineales e invariantes en el tiempo en TD nivel intermedio:
-
Si la respuesta al impulso es
- Obtenga H(z) y diga si es o no estable el sistema.
- Determine el diagrama de bloques del sistema.
- Obtenga los primeros 5 valores de h[n] mediante recursividad.
- Obtenga la respuesta al escalón mediante convolución.
-
Para los sistemas de tiempo discreto, establecidos mediante la función de transferencia: Determine
- La respuesta al impulso.
- La respuesta al escalón.
- El diagrama de polos y ceros.
- El diagrama de bloques.
-
Si la respuesta al impulso es
- Obtenga H(z) y diga si es o no estable el sistema.
- Determine el diagrama de bloques del sistema.
- Obtenga los primeros 5 valores de h[n] mediante recursividad.
- Obtenga la respuesta al escalón mediante convolución.
-
Para los sistemas de tiempo discreto, establecidos mediante la función de transferencia: Determine
- La respuesta al impulso.
- La respuesta al escalón.
- El diagrama de polos y ceros.
- El diagrama de bloques.
-
Si la respuesta al impulso es
- Obtenga H(z) y diga si es o no estable el sistema.
- Determine el diagrama de bloques del sistema.
- Obtenga los primeros 5 valores de h[n] mediante recursividad.
- Obtenga la respuesta al escalón mediante convolución.
-
Para los sistemas de tiempo discreto, establecidos mediante la función de transferencia: Determine
- La respuesta al impulso,
- La respuesta al escalón,
- El diagrama de polos y ceros,
- El diagrama de bloques.
-
Si la respuesta al impulso es
- Obtenga H(z) y diga si es o no estable el sistema.
- Determine el diagrama de bloques del sistema.
- Obtenga los primeros 5 valores de h[n] mediante recursividad.
- Obtenga la respuesta al escalón mediante convolución.
-
Para los sistemas de tiempo discreto, establecidos mediante la función de transferencia: Determine
- La respuesta al impulso.
- La respuesta al escalón.
- El diagrama de polos y ceros.
- El diagrama de bloques.
-
Si la respuesta al impulso es
- Obtenga H(z) y diga si es o no estable el sistema.
- Determine el diagrama de bloques del sistema.
- Obtenga los primeros 5 valores de h[n] mediante recursividad.
- Obtenga la respuesta al escalón mediante convolución.
-
Para los sistemas de tiempo discreto, establecidos mediante la función de transferencia: Determine
- La respuesta al impulso,
- La respuesta al escalón,
- El diagrama de polos y ceros,
- El diagrama de bloques.
-
Si la respuesta al impulso es
- Obtenga H(z) y diga si es o no estable el sistema.
- Determine el diagrama de bloques del sistema.
- Obtenga los primeros 5 valores de h[n] mediante recursividad.
- Obtenga la respuesta al escalón mediante convolución.
-
Para los sistemas de tiempo discreto, establecidos mediante la función de transferencia: Determine
- La respuesta al impulso.
- La respuesta al escalón.
- El diagrama de polos y ceros.
- El diagrama de bloques.
Sistemas lineales e invariantes en el tiempo en TD nivel avanzado:
-
Si la respuesta al impulso es
- Obtenga H(z) y diga si es o no estable el sistema.
- Determine el diagrama de bloques del sistema.
- Obtenga los primeros 5 valores de h[n] mediante recursividad.
- Obtenga la respuesta al escalón mediante convolución.
-
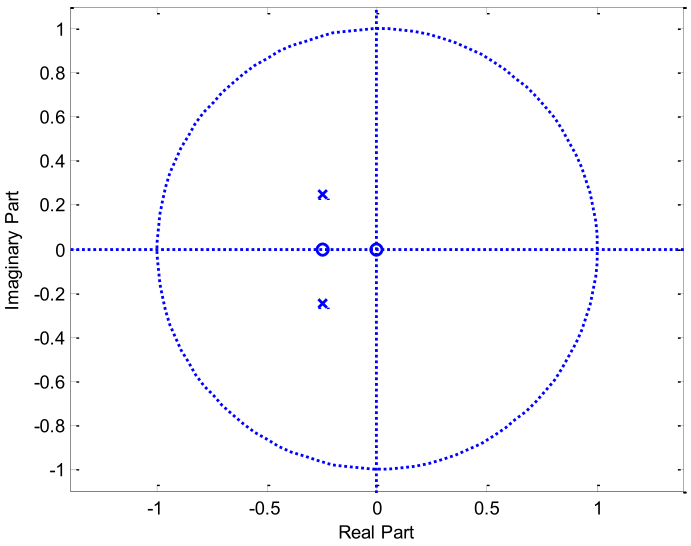
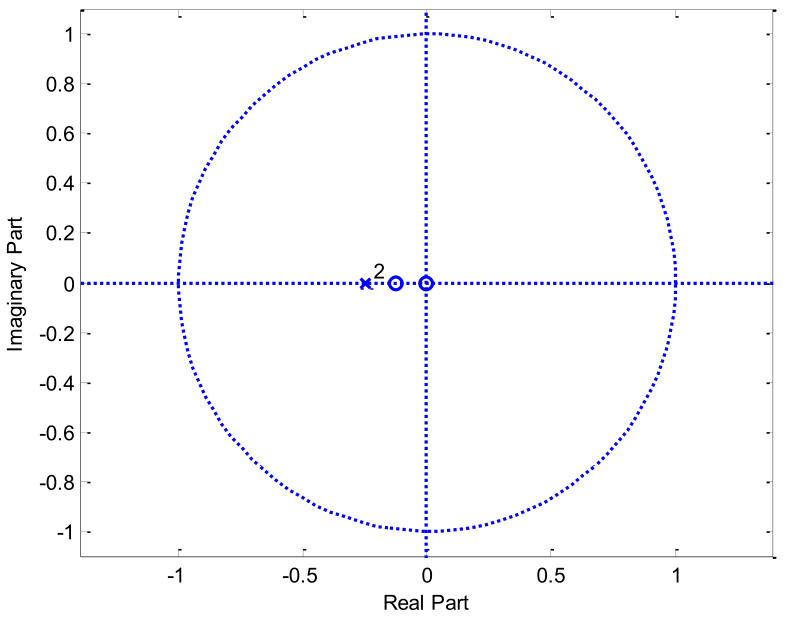
Para el sistema de tiempo discreto, establecido mediante el diagrama de polos y ceros, con ganancia 2: Determine
- La función de transferencia.
- La respuesta al impulso.
- La respuesta al escalón.
-
El diagrama de bloques.
-
Si la respuesta al impulso es
- Obtenga H(z) y diga si es o no estable el sistema.
- Determine el diagrama de bloques del sistema.
- Obtenga los primeros 5 valores de h[n] mediante recursividad.
- Obtenga la respuesta al escalón mediante convolución.
-
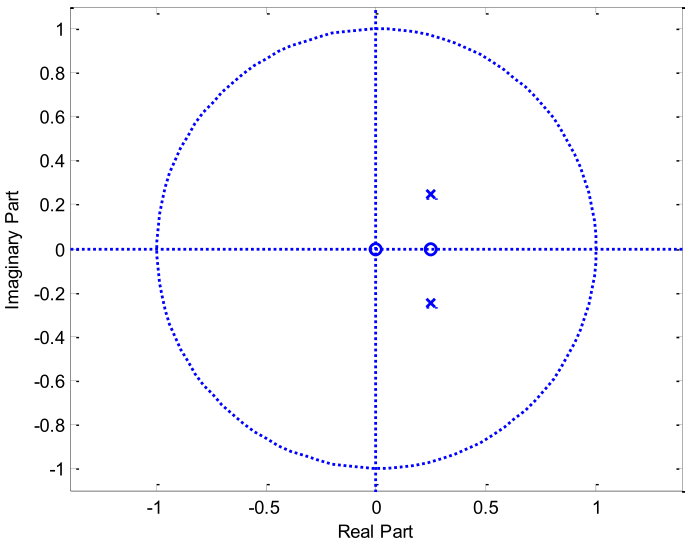
Para el sistema de tiempo discreto, establecido mediante el diagrama de polos y ceros, con ganancia 2: Determine
- La función de transferencia.
- La respuesta al impulso.
- La respuesta al escalón.
-
El diagrama de bloques.
-
Si la respuesta al impulso es
- Obtenga H(z) y diga si es o no estable el sistema.
- Determine el diagrama de bloques del sistema.
- Obtenga los primeros 5 valores de h[n] mediante recursividad.
- Obtenga la respuesta al escalón mediante convolución.
-
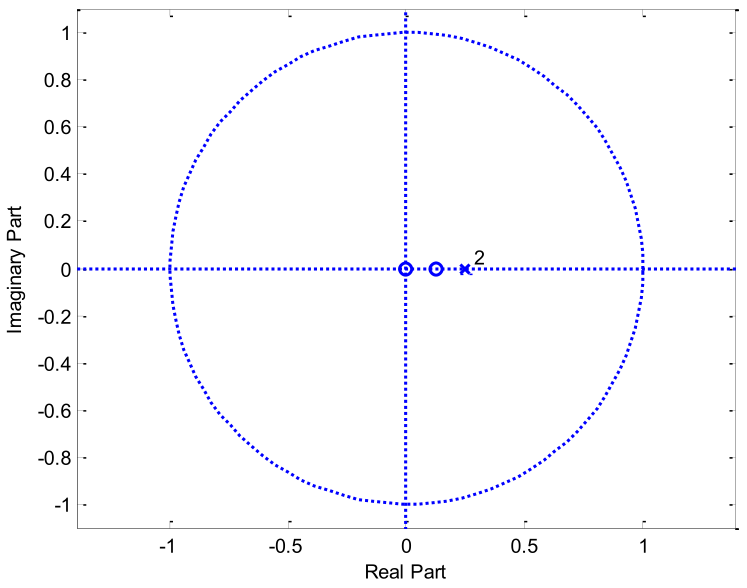
Para el sistema de tiempo discreto, establecido mediante el diagrama de polos y ceros, con ganancia 2: Determine
- La función de transferencia.
- La respuesta al impulso.
- La respuesta al escalón.
-
El diagrama de bloques.
-
Para el sistema de tiempo discreto, establecido mediante el diagrama de polos y ceros, con ganancia 2: Determine
- La función de transferencia.
- La respuesta al impulso.
- La respuesta al escalón.
-
El diagrama de bloques.
-
Si la respuesta al impulso es
-
- Obtenga la respuesta de un sistema en tiempo discreto a una entrada escalón mediante convolución.
- Verifique la respuesta mediante recursividad.
-
-
Presente las siguientes propiedades de la transformada Z y un ejemplo de aplicación:
- Multiplicación por .
- Multiplicación por .
- Inversión en el tiempo .
-
La función de transferencia de un sistema de 2○ orden es
- Obtenga la expresión de la ecuación en diferencias del sistema.
- Determine la respuesta al impulso h[n] mediante recursividad para los primeros 5 valores.
- Determine la respuesta al impulso h[n] a partir de la función de transferencia.
- Determine el diagrama de polos y ceros e identifique si el sistema es o no estable.
-
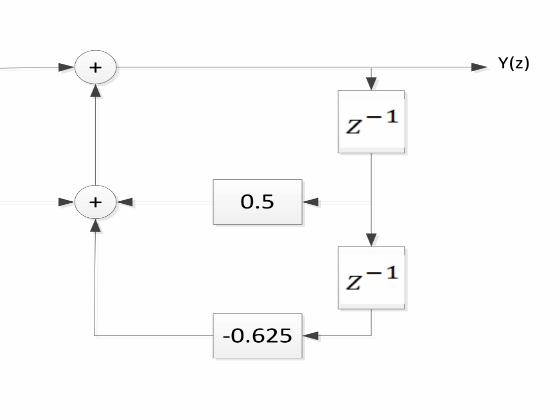
Para el sistema de tiempo discreto, establecido mediante el diagrama de bloques.Determine
- La función de transferencia.
- La respuesta al impulso.
- La respuesta al escalón.
-
El diagrama de polos y ceros.
-
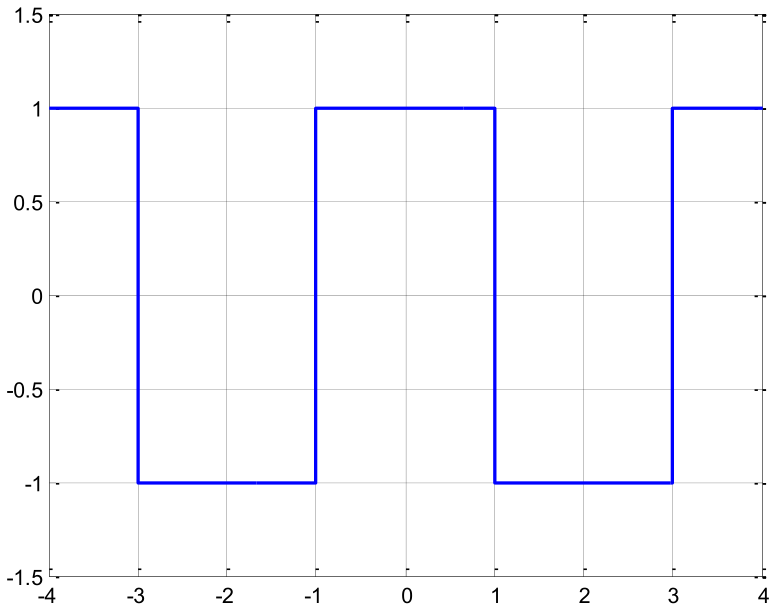
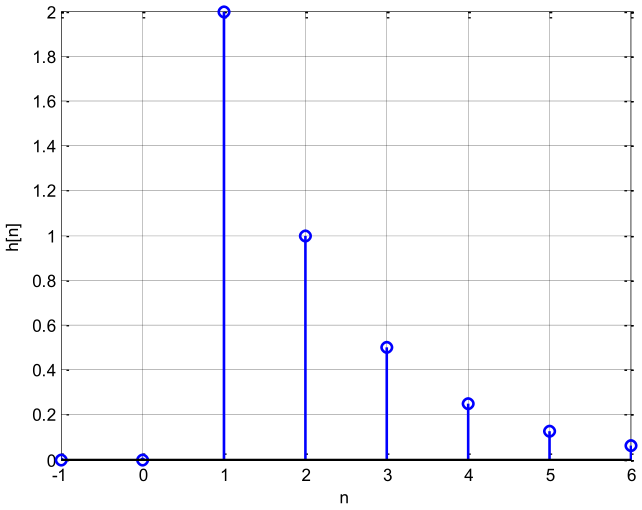
La figura muestra la respuesta al impulso de un sistema.
- Identifique y presente la expresión de la respuesta al impulso de la figura.
-
Obtenga la respuesta del sistema, si la entrada es:.
-
Obtenga mediante TZ la respuesta a una entrada escalón.
Serie de Fourier de TC:
En los ejercicios propuestos de esta sección el estudiante será capaz de obtener la representación en serie de Fourier de diversas señales, identificará y analizará los sistemas desde el punto de vista de filtrado y obtendrá las respuestas. Reafirmará el conocimiento de análisis en el dominio de la frecuencia. Podrá verificar el análisis y las respuestas mediante simulaciones.
Selecciona la dificultad en las caritas de la izquierda.
Serie de Fourier de TC nivel principiante:
-
Para la funci√≥n con periodo T‚ÄÖ=‚ÄÖ6 definida por segmentos como x(t)‚ÄÖ=‚ÄÖ‚éß‚é™‚é®‚é™‚é© 0.5cos‚éõ‚éù(œÄt)/(3)‚éû‚éÝ ‚ÄÖ‚àí‚ÄÖ1.5‚Äւ⧂ÄÖt‚Äւ⧂ÄÖ1.5 ‚ÄÖ ‚ÄÖ ‚ÄÖ ‚ÄÖ ‚ÄÖ ‚ÄÖ 0 ‚ÄÖotro valor
- Obtener de forma analítica los coeficientes ak.
- Obtener la gr√°fica de la magnitud de los coeficientes ak.
- Expresar la señal x(t) como una suma de exponenciales complejas.
- Graficar la señal anterior para diferentes valores de k y verificar que se aproxima a x(t).
-
Grafique la señal x(t) = cos(2πt) + cos(50πt)
- Obtenga y grafique el espectro discreto de x(t) = cos(2πt) + cos(50πt).
-
Filtre la señal x(t) = cos(2πt) + cos(50πt) a través de un filtro Butterworth de manera que separe y obtenga.x1(t) = cos(2πt)x2(t) = cos(50πt)
- Presente el modelo del filtro seleccionado.
- Grafique la respuesta en frecuencia, en magnitud y fase, del filtro seleccionado.
-
Grafique la señal x(t) = ∑∞m =  − ∞tri(t − 2m)
- Obtenga y grafique el espectro discreto de x(t).
- Filtre la señal x(t) a través de un filtro Butterworth de manera que separe y obtenga las tres primeras armónicas.
- Presente el modelo del filtro seleccionado.
- Grafique la respuesta en frecuencia, en magnitud y fase, del filtro seleccionado.
-
Grafique la señal x(t) = ∑∞m =  − ∞rect(t − 4m)
- Obtenga y grafique el espectro discreto de x(t).
- Filtre la señal x(t) a través de un filtro Butterworth de manera que elimine la componente de directa.
- Presente el modelo del filtro seleccionado.
- Grafique la respuesta en frecuencia, en magnitud y fase, del filtro seleccionado.
-
Grafique la señal x(t) = ∑∞m =  − ∞rect(t − 4m)
- Obtenga y grafique el espectro discreto de x(t).
- Filtre la señal x(t) del ejercicio 2 a través de un filtro Butterworth de manera que obtenga solo la primera armónica.
- Presente el modelo del filtro seleccionado.
- Grafique la respuesta en frecuencia, en magnitud y fase, del filtro seleccionado.
-
Grafique la señal x(t) = (∑∞m =  − ∞rect(t − 4m)) + 0.1cos(50πt)
- Obtenga y grafique el espectro discreto de x(t).
- Filtre la señal x(t) a través de un filtro Butterworth de manera que obtenga solo ∑∞m =  − ∞rect(t − 4m)
- Presente el modelo del filtro seleccionado.
- Grafique la respuesta en frecuencia, en magnitud y fase, del filtro seleccionado.
-
Grafique la señal x(t) = cos(2πt) + 0.1cos(50πt)
- Obtenga y grafique el espectro discreto de x(t).
- Filtre la señal x(t) a través de un filtro Butterworth de manera que obtenga solo x(t) = cos(2πt)
- Presente el modelo del filtro seleccionado.
- Grafique la respuesta en frecuencia, en magnitud y fase, del filtro seleccionado.
-
Grafique la señal x(t) = (∑∞m =  − ∞tri(t − 4m)) + 0.5cos(10πt)
- Obtenga y grafique el espectro discreto de x(t).
- Filtre la señal x(t) a través de un filtro Butterworth de manera que obtenga solo x(t) = ∑∞m =  − ∞tri(t − 4m)
- Presente el modelo del filtro seleccionado.
- Grafique la respuesta en frecuencia, en magnitud y fase, del filtro seleccionado.
-
Los coeficientes de la serie de Fourier de una señal x(t) periódica con periodo T = 4 son los siguientes:ak = ⎧⎪⎨⎪⎩ 1,   k par             2,   k impar  
- Grafique el espectro discreto de x(t).
- Obtenga y grafique la señal x(t).
- Filtre la señal x(t) a través de un filtro Butterworth de manera que elimine la componente de directa y la primera armónica.
- Presente el modelo del filtro seleccionado.
- Grafique la respuesta en frecuencia, en magnitud y fase, del filtro seleccionado.
-
Los coeficientes de la serie de Fourier de una se√±al x(t) peri√≥dica con periodo T‚ÄÖ=‚ÄÖ8 son los siguientes:|ak|‚ÄÖ=‚ÄÖ‚éß‚é™‚é®‚é™‚é© 2,‚ÄÖ k‚ÄÖ=‚ÄÖ0 ‚ÄÖ ‚ÄÖ ‚ÄÖ ‚ÄÖ ‚éõ‚éù(1)/(2)‚éû‚éÝ|k|,‚ÄÖ k‚ÄÖ‚âÝ‚ÄÖ0
- Grafique el espectro discreto de x(t).
- Obtenga y grafique la señal x(t).
- Filtre la señal x(t) a través de un filtro Butterworth de manera que elimine la componente de directa y la primera armónica.
- Presente el modelo del filtro seleccionado.
- Grafique la respuesta en frecuencia, en magnitud y fase, del filtro seleccionado.
-
Una señal periódica continua x(t) tiene un periodo fundamental de T = 8. Los coeficientes de la serie de Fourier diferentes de cero para x(t) son: a1 = a − 1 = 2     a3 = a∗ − 3 = j4
- Exprese x(t) en una serie de cosenos.
- Verifique la solución con Matlab.
-
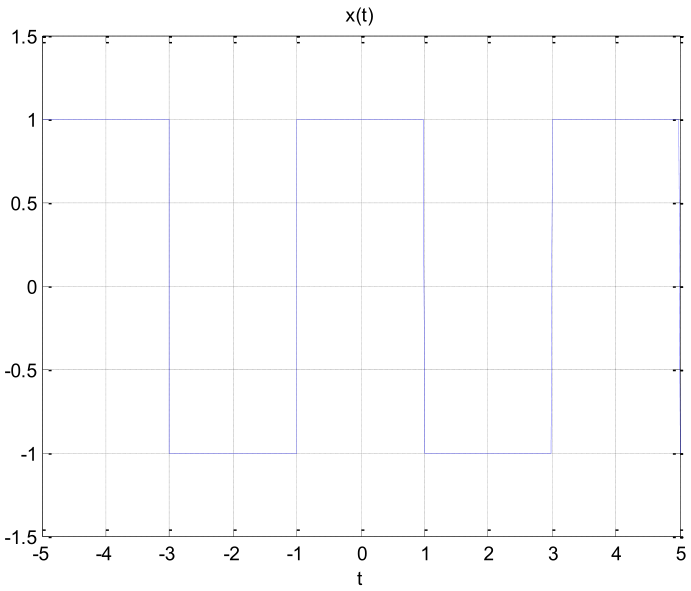
Considere la se√±al cuadrada x(t) con periodo T: x(t)‚ÄÖ=‚ÄÖ‚éß‚é™‚é®‚é™‚é© 1 |t|‚ÄÖ<‚ÄÖT1 ‚ÄÖ ‚ÄÖ ‚ÄÖ ‚ÄÖ 0 ‚ÄÖotro valorcuyos coeficientes de la serie exponencial de Fourier son:ak‚ÄÖ=‚ÄÖ(sin(kœâ0T1))/(kœÄ) k‚ÄÖ‚âÝ‚ÄÖ0Si x1(t) es como esta expresada, aplique las propiedades de serie de Fourier para determinar los coeficientes de x1(t).x1(t)‚ÄÖ=‚ÄÖ‚éß‚é™‚é®‚é™‚é© 1.5 0‚Äւ⧂ÄÖt‚ÄÖ<‚ÄÖ1 ‚ÄÖ ‚ÄÖ ‚ÄÖ ‚ÄÖ ‚ÄÖ‚àí‚ÄÖ1.5 1‚Äւ⧂ÄÖt‚ÄÖ<‚ÄÖ2Verifique la soluci√≥n con Matlab.
-
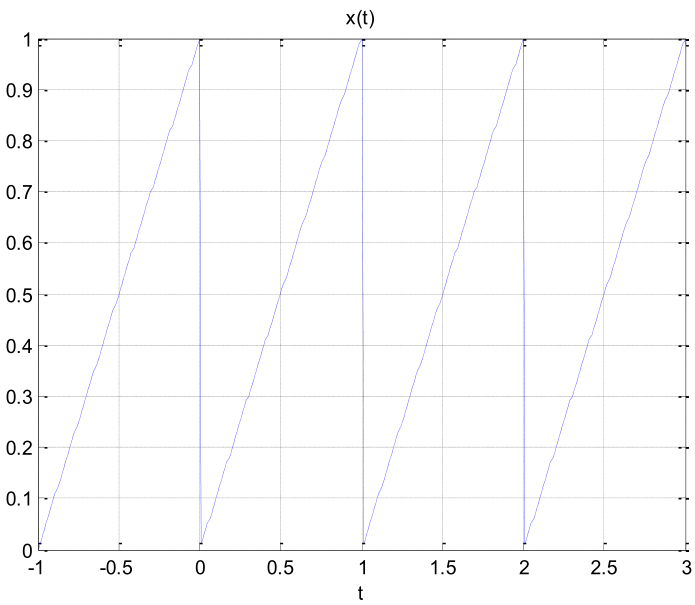
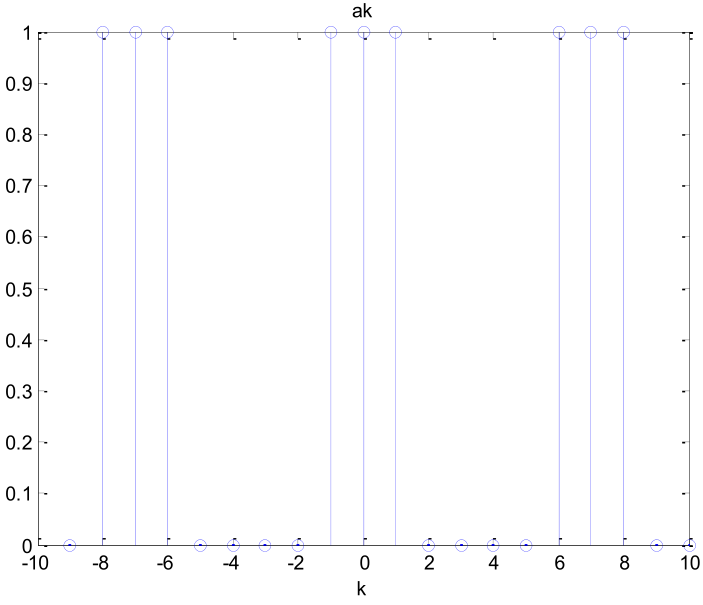
C.5 Los coeficientes espectrales de la serie de Fourier para la se√±al peri√≥dica x(t) mostrada son los siguientes: ak‚ÄÖ=‚ÄÖ(2)/(kœÄ)sin‚éõ‚éù(kœÄ)/(2)‚éû‚éÝ k‚ÄÖ‚âÝ‚ÄÖ0
-
Aplicando la propiedad de desplazamiento en el tiempo indicada, determine los coeficientes para la señal x(t − 0.5) x(t − t0)⟶a − jkω0t0ke
- Grafique el espectro de los coeficientes de la señal x(t − 0.5)
- Obtenga la expresión de la señal x(t − 0.5) como una aproximación mediante a serie de Fourier de cosenos.
-
Aplicando la propiedad de desplazamiento en el tiempo indicada, determine los coeficientes para la señal x(t − 0.5)
-
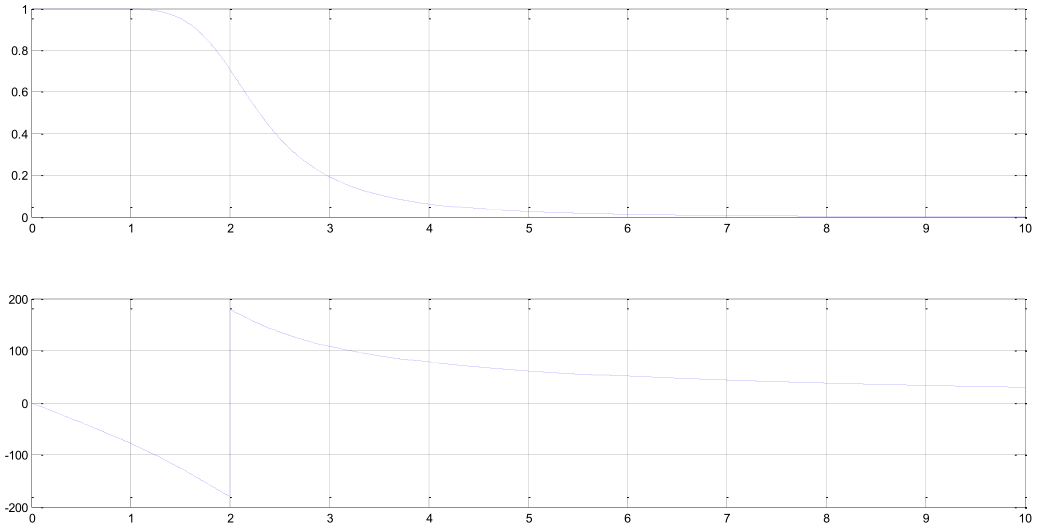
Considere la siguiente señal, la cual pasa por un filtro cuya respuesta en frecuencia es la mostrada.
-
Determine la salida del filtro tomando los valores aproximados de las gr√°ficas de la respuesta en frecuencia. Identifique en la gr√°fica los valores propios. x(t)‚ÄÖ=‚ÄÖ3cos‚éõ‚éù(2œÄ)/(20) t‚éû‚éÝ‚ÄÖ+‚ÄÖ2cos‚éõ‚éù(œÄ)/(2) t‚ÄÖ+‚ÄÖ(œÄ)/(4)‚éû‚éÝ‚ÄÖ+‚ÄÖcos‚éõ‚éù(œÄ)/(10) t‚ÄÖ+‚ÄÖ(œÄ)/(8)‚éû‚éÝ
- Exprese su interpretación de la respuesta obtenida.
-
Determine la salida del filtro tomando los valores aproximados de las gr√°ficas de la respuesta en frecuencia. Identifique en la gr√°fica los valores propios.
-
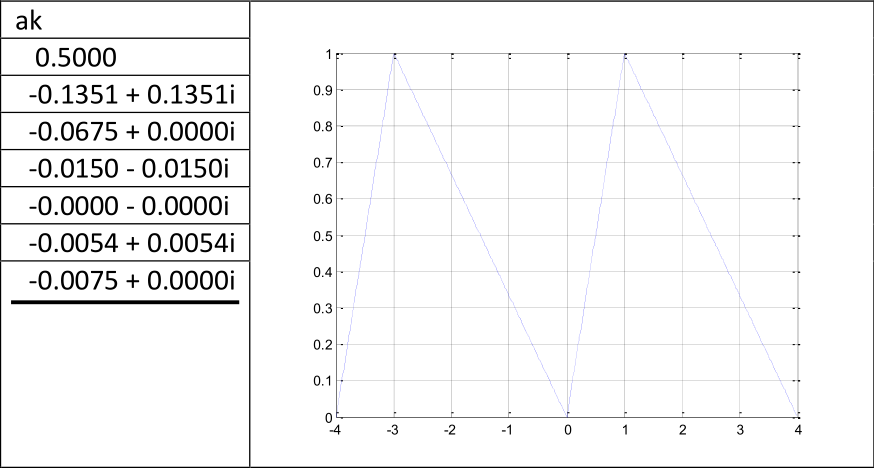
Los primeros 7 coeficientes ak de la señal x(t) obtenidos con Matlab son los siguientes:
- Determine el diagrama espectral de la señal con los coeficientes ak.
- Obtenga la expresión de la señal mediante una serie de cosenos.
-
Grafique la señal x(t) = cos(2πt) + cos(50πt)
- Obtenga y grafique el espectro discreto de x(t) = cos(2πt) + cos(50πt).
-
Filtre la señal x(t) = cos(2πt) + cos(50πt) a través de un filtro Butterworth de manera que separe y obtenga.x1(t) = cos(2πt)x2(t) = cos(50πt)
- Presente el modelo del filtro seleccionado.
- Grafique la respuesta en frecuencia, en magnitud y fase, del filtro seleccionado.
-
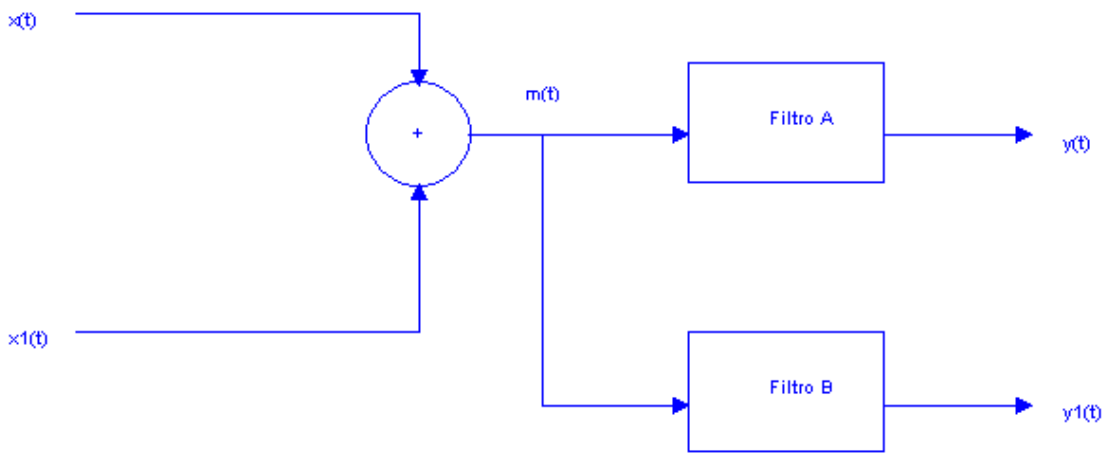
Considere las señales x(t) y x1(t). x1(t) = (1)/(20)cos(10πt)
- Grafique x(t), x1(t) y m(t).
- Grafique el espectro de x(t), x1(t) y m(t).
- Seleccione los filtros Butterwoth apropiados de manera que y(t)‚ÄÖ=‚ÄÖx(t) y y1(t)‚ÄÖ=‚ÄÖx1(t).
Serie de Fourier de TC nivel intermedio:
-
Grafique la señal x(t) = ∑∞m =  − ∞tri(t − 2m)
- Obtenga y grafique el espectro discreto de x(t).
- Filtre la señal x(t) a través de un filtro Butterworth de manera que separe y obtenga las tres primeras armónicas.
- Presente el modelo del filtro seleccionado.
- Grafique la respuesta en frecuencia, en magnitud y fase, del filtro seleccionado.
-
Grafique la señal x(t) = ∑∞m =  − ∞rect(t − 4m)
- Obtenga y grafique el espectro discreto de x(t).
- Filtre la señal x(t) a través de un filtro Butterworth de manera que elimine la componente de directa.
- Presente el modelo del filtro seleccionado.
- Grafique la respuesta en frecuencia, en magnitud y fase, del filtro seleccionado.
-
Considere las señales x(t) y x1(t).
 x1(t) = (1)/(20)cos(30πt)
x1(t) = (1)/(20)cos(30πt)- Grafique x(t), x1(t) y m(t).
- Grafique el espectro de x(t), x1(t) y m(t).
-
Seleccione los filtros Butterwoth apropiados de manera que y(t) = x(t) y y1(t) = x1(t).∗Puede utilizar la función tripuls( )
-
Grafique la señal x(t) = ∑∞m =  − ∞rect(t − 4m)
- Obtenga y grafique el espectro discreto de x(t).
- Filtre la señal x(t) a través de un filtro Butterworth de manera obtenga sólo la primera armónica.
- Presente el modelo del filtro seleccionado.
- Grafique la respuesta en frecuencia, en magnitud y fase, del filtro seleccionado.
-
Considere las señales x(t) y x1(t).

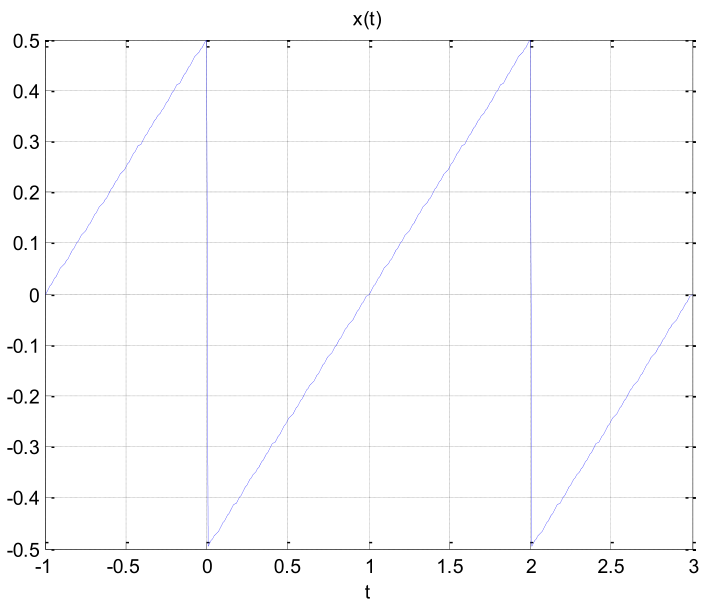 x1(t) = (1)/(20)cos(40πt)
x1(t) = (1)/(20)cos(40πt)- Grafique x(t), x1(t) y m(t).
- Grafique el espectro de x(t), x1(t) y m(t).
-
Seleccione los filtros Butterwoth apropiados de manera que y(t) = x(t) y y1(t) = x1(t).∗Puede utilizar la función tripuls( )
-
Considere las señales x(t) y x1(t).

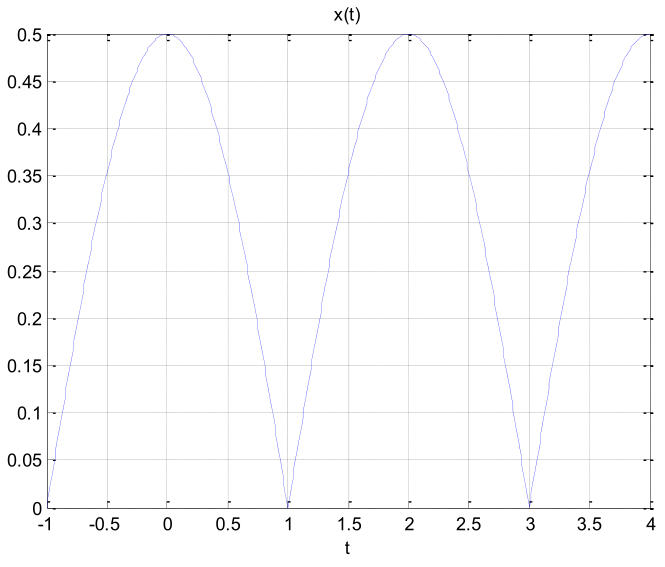 x1(t) = (1)/(20)cos(40πt)
x1(t) = (1)/(20)cos(40πt)- Grafique x(t), x1(t) y m(t).
- Grafique el espectro de x(t), x1(t) y m(t).
- Seleccione los filtros Butterwoth apropiados de manera que y(t)‚ÄÖ=‚ÄÖx(t) y y1(t)‚ÄÖ=‚ÄÖx1(t).
-
Grafique la señal x(t) = cos(2πt) + 0.1cos(50πt)
- Obtenga y grafique el espectro discreto de x(t).
-
Filtre la señal x(t) a través de un filtro Butterworth de manera que obtenga sólo x(t) = cos(2πt)
- Presente el modelo del filtro seleccionado.
- Grafique la respuesta en frecuencia, en magnitud y fase, del filtro seleccionado.
-
Considere las señales x(t) y x1(t).
 x(t) = 2cos(2πt)x1(t) = 2cos(6πt)
x(t) = 2cos(2πt)x1(t) = 2cos(6πt)- Grafique x(t), x1(t) y m(t).
- Grafique el espectro de x(t), x1(t) y m(t).
- Seleccione los filtros Butterwoth apropiados de manera que y(t)‚ÄÖ=‚ÄÖx(t) y y1(t)‚ÄÖ=‚ÄÖx1(t).
-
Grafique la señal x(t) = (∑∞m =  − ∞tri(t − 4m)) + .05cos(10πt)
- Obtenga y grafique el espectro discreto de x(t).
-
Filtre la señal x(t) a través de un filtro Butterworth de manera que obtenga sólo ∑∞m =  − ∞tri(t − 4m)
- Presente el modelo del filtro seleccionado.
- Grafique la respuesta en frecuencia, en magnitud y fase, del filtro seleccionado.
-
Considere las señales x(t) y x1(t).
 x(t) = 2cos(2πt)x1(t) = 4cos(6πt) + 6cos(10πt)
x(t) = 2cos(2πt)x1(t) = 4cos(6πt) + 6cos(10πt)- Grafique x(t), x1(t) y m(t).
- Grafique el espectro de x(t), x1(t) y m(t).
- Seleccione los filtros Butterwoth apropiados de manera que y(t) = x(t) y y1(t) = 4cos(6πt).
-
Los coeficientes de la serie de Fourier de una se√±al x(t) peri√≥dica con periodo T‚ÄÖ=‚ÄÖ4 son los siguientes: ak‚ÄÖ=‚ÄÖ‚éß‚é™‚é®‚é™‚é© 1 k¬Ýpar ‚ÄÖ ‚ÄÖ ‚ÄÖ ‚ÄÖ [‚ÄÖ‚àí‚ÄÖ2mm]2 k¬Ýimpar
- Grafique el espectro discreto de x(t).
- Obtenga y grafique la señal x(t).
- Filtre la señal x(t) a través de un filtro Butterworth de manera que elimine la componente de directa y la primera armónica.
- Presente el modelo del filtro seleccionado.
- Grafique la respuesta en frecuencia, en magnitud y fase, del filtro seleccionado.
-
Considere las señales x(t) y x1(t).
 x1(t) = 4cos(2πt)
x1(t) = 4cos(2πt)- Grafique x(t), x1(t) y m(t).
- Grafique el espectro de x(t), x1(t) y m(t).
-
Seleccione los filtros Butterwoth apropiados de manera que y(t) = x(t) y y1(t) = 4cos(6πt).∗Puede utilizar la función square( )
-
Los coeficientes de la serie de Fourier de una se√±al x(t) peri√≥dica con periodo T‚ÄÖ=‚ÄÖ8 son los siguientes: |ak|‚ÄÖ=‚ÄÖ‚éß‚é™‚é®‚é™‚é© 2,‚ÄÖ k‚ÄÖ=‚ÄÖ0 ‚ÄÖ ‚ÄÖ ‚ÄÖ ‚ÄÖ ‚éõ‚éù(1)/(2)‚éû‚éÝ|k|,‚ÄÖ k‚ÄÖ‚âÝ‚ÄÖ0
- Grafique el espectro discreto de x(t).
- Obtenga y grafique la señal x(t).
- Filtre la señal x(t) a través de un filtro Butterworth de manera que elimine la componente de directa y la primera armónica.
- Presente el modelo del filtro seleccionado.
- Grafique la respuesta en frecuencia, en magnitud y fase, del filtro seleccionado.
-
Considere la se√±al cuadrada x(t) con periodo T: x(t)‚ÄÖ=‚ÄÖ‚éß‚é®‚é© 1 |t|‚ÄÖ<‚ÄÖT1 ‚ÄÖ ‚ÄÖ [3mm]0 ‚ÄÖotro valorcuyos coeficientes de la serie de Fourier son:ak‚ÄÖ=‚ÄÖ(sin(kœâ0T1))/(kœÄ) k‚ÄÖ‚âÝ‚ÄÖ0
-
Si x1(t) es como esta expresada, aplique las propiedades de serie de Fourier para determinar los coeficientes de x1(t) con base en los coeficientes de x(t). x1(t) = ⎧⎨⎩ 1.5 0 ≤ t < 1     [3mm] − 1.5 1 ≤ t < 2
-
Si x1(t) es como esta expresada, aplique las propiedades de serie de Fourier para determinar los coeficientes de x1(t) con base en los coeficientes de x(t).
-
Considere las señales x(t) y x1(t).

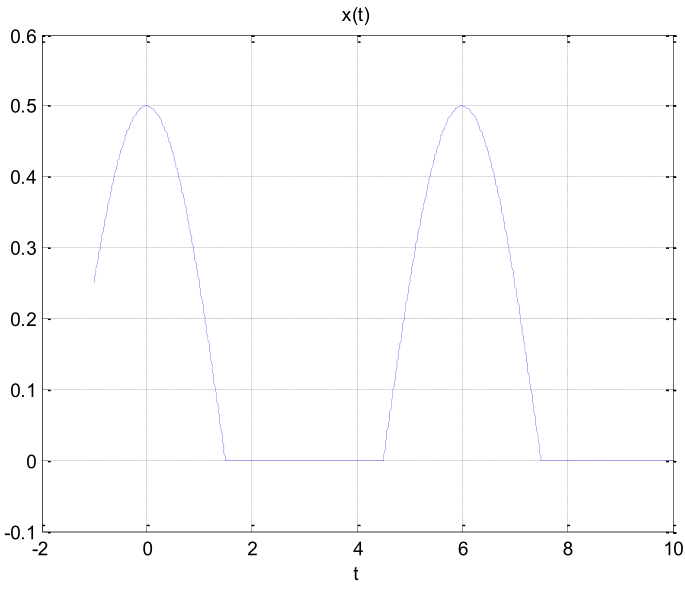 x1(t) = (1)/(20)cos(10πt)
x1(t) = (1)/(20)cos(10πt)
- Grafique x(t), x1(t) y m(t).
- Grafique el espectro de x(t), x1(t) y m(t).
- Seleccione los filtros Butterwoth apropiados de manera que y(t)‚ÄÖ=‚ÄÖx(t) y y1(t)‚ÄÖ=‚ÄÖx1(t).
-
Una señal periódica continua x(t) tiene un periodo fundamental de T = 8. Los coeficientes de la serie de Fourier diferentes de cero para x(t) son: a1 = a − 1 = 2   [3mm]a3 = a∗ − 3 = j4   [3mm]a5 = a∗ − 5 = 2 − j4
- Exprese x(t) en una serie de cosenos.
- Grafique la señal.
-
Considere las señales x(t) y x1(t).

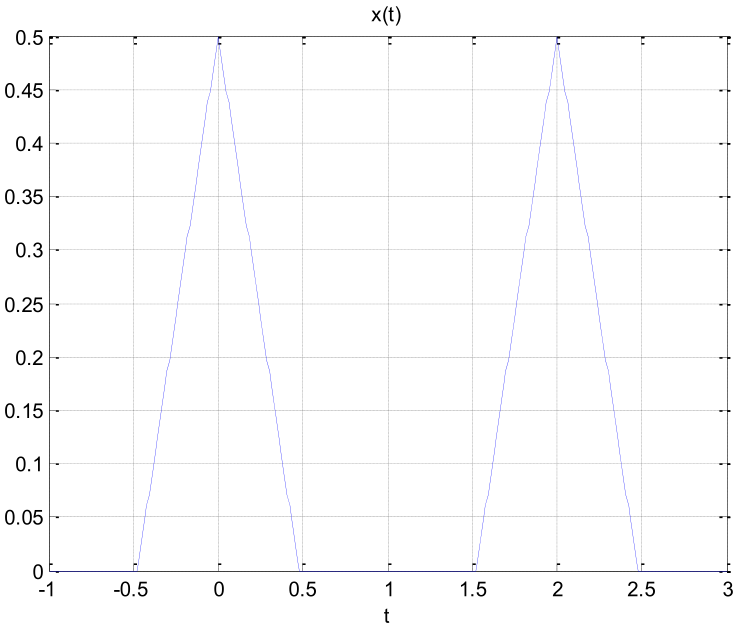 x1(t) = (1)/(20)cos(30πt)
x1(t) = (1)/(20)cos(30πt)- Grafique x(t), x1(t) y m(t).
- Grafique el espectro de x(t), x1(t) y m(t).
-
Seleccione los filtros Butterwoth apropiados de manera que y(t) = x(t) y y1(t) = x1(t).∗Puede utilizar la función tripuls( )
Serie de Fourier de TC nivel avanzado:
-
Usando suma de señales, escriba el código para encontrar:
- El tramo de la señal de ECG P y PQ.
- La señal QRS.
- La Señal T.
-
Realice los cálculo necesarios para encontrar los coeficientes de la Serie Trigonométrica de Fourier de:
- Encuentre los coeficientes a0, an y bn de la señal P y PQ.
- Encuentre los coeficientes a0, an y bn de la señal QRS.
- Encuentre los coeficientes a0, an y bn de la señal T.
-
Escriba y verifique los códigos necesarios para calcular la STF para 30 componentes frecuenciales de
- La señal P y PQ.
- La señal QRS.
- La señal T.
Análisis de Fourier en TD:
En los ejercicios propuestos de esta sección el estudiante será capaz de obtener la representación en serie de Fourier de diversas señales, identificará y analizará los sistemas desde el punto de vista de filtrado y obtendrá las respuestas. Reafirmará el conocimiento de análisis en el dominio de la frecuencia. Podrá verificar el análisis y las respuestas mediante simulaciones.
Selecciona la dificultad en las caritas de la izquierda.
Análisis de Fourier en TD: nivel principiante:
Mediante las funciones butter() y freqz(), obtenga los siguientes filtros:
- Obtenga la expresión de la respuesta en frecuencia para un filtro digital Butterworth paso baja de segundo orden con una frecuencia de corte π ⁄ 2 y grafique la respuesta en frecuencia en amplitud. Verifique la frecuencia de corte.
- Repita el ejercicio 1) para un filtro digital Butterworth paso baja de cuarto orden con una frecuencia de corte π ⁄ 2 .
- Repita el ejercicio 1) para un filtro digital Butterworth paso banda de segundo orden, cuyas frecuencias de corte son ωc1 = 2π ⁄ 10 y ωc2 = 3π ⁄ 10 .
- Repita el ejercicio 3) con frecuencias de corte de ωc1 = 4π ⁄ 10 y ωc2 = 6π ⁄ 10.
- Repita el ejercicio 3) para un filtro digital Butterworth supresor de banda de segundo orden, cuyas frecuencias de corte son ωc1 = 5π ⁄ 10 y ωc2 = 8π ⁄ 10.
-
Repita el ejercicio 1) para un filtro digital Butterworth paso alta de segundo orden y una frecuencia de corte 9π ⁄ 10..
Análisis de Fourier en TD: nivel intermedio:
-
Una señal periódica discreta x[n] con periodo fundamental de N = 5. Los coeficientes de la serie exponencial de Fourier diferentes de cero para x[n] son:a0 = 1     a2 = a∗ − 2 = 4e(jπ)/(3)     a4 = a∗ − 4 = 3e(jπ)/(2)
- Exprese x[n] en una serie de cosenos.
- Verifique la solución con Matlab.
-
Una señal periódica discreta x[n] tiene un periodo fundamental de N = 7. Los coeficientes de la serie de Fourier diferentes de cero para x[n] son: a8 = j     a9 = j2     a10 = j3
- Obtenga la expresión de x[n].
- Determine los valores de a0,‚ÄÖ a‚ÄÖ‚àí‚ÄÖ1,‚ÄÖ a‚ÄÖ‚àí‚ÄÖ2,‚ÄÖ a‚ÄÖ‚àí‚ÄÖ3,‚ÄÖ a‚ÄÖ‚àí‚ÄÖ4,‚ÄÖ a‚ÄÖ‚àí‚ÄÖ5,‚ÄÖ a‚ÄÖ‚àí‚ÄÖ6,‚ÄÖ a‚ÄÖ‚àí‚ÄÖ7.
- Verifique la solución con Matlab.
-
Una señal periódica continua x[n] con periodo fundamental de N = 5. Los coeficientes de la serie exponencial de Fourier diferentes de cero para x[n] son:a0 = 1     a2 = a∗ − 2 = e(jπ)/(4)     a4 = a∗ − 4 = 2e(jπ)/(3)
- Grafique el espectro de los coeficientes con k‚ÄÖ=‚ÄÖ0 en el centro.
- Exprese x[n] en una serie de cosenos y grafique la señal.
-
Los coeficientes espectrales de una se√±al x[n] peri√≥dica est√°n dados por: ak‚ÄÖ=‚ÄÖsin‚éõ‚éù(kœÄ)/(3)‚éû‚éÝ 0‚Äւ⧂ÄÖk‚Äւ⧂ÄÖ6
- Grafique el espectro con los coeficientes ak
- Obtenga la expresión para x[n] cuyo espectro es el especificado.
- Seleccione los filtros Butterwoth apropiados de manera que y[n] incluya las componentes de la 1a y 2a armónica.
-
Los coeficientes espectrales de una se√±al x[n] peri√≥dica est√°n dados por: ak‚ÄÖ=‚ÄÖsin‚éõ‚éù(kœÄ)/(3)‚éû‚éÝ 0‚Äւ⧂ÄÖk‚Äւ⧂ÄÖ6
- Grafique el espectro con los coeficientes ak
- Obtenga la expresión para x[n] cuyo espectro es el especificado.
- Seleccione los filtros Butterwoth apropiados de manera que y[n] incluya las componentes de la 1a y 2a armónica.
-
Los coeficientes espectrales de una se√±al x[n] peri√≥dica est√°n dados por: ak‚ÄÖ=‚ÄÖsin‚éõ‚éù(kœÄ)/(3)‚éû‚éÝ 0‚Äւ⧂ÄÖk‚Äւ⧂ÄÖ6
- Grafique el espectro con los coeficientes ak
- Obtenga la expresión para x[n] cuyo espectro es el especificado.
- Seleccione los filtros Butterwoth apropiados de manera que y[n] incluya las componentes de la 1a y 2a armónica.
-
Una señal periódica discreta x[n] tiene un periodo fundamental de N = 7. Los coeficientes de la serie de Fourier diferentes de cero para x[n] son:a15 = j     a16 = j2     a17 = j3
- Obtenga la expresión de x[n].
- Determine los valores de a0,‚ÄÖ a‚ÄÖ‚àí‚ÄÖ1,‚ÄÖ a‚ÄÖ‚àí‚ÄÖ2,‚ÄÖ a‚ÄÖ‚àí‚ÄÖ3
-
Los coeficientes espectrales de una se√±al x[n] peri√≥dica con N‚ÄÖ=‚ÄÖ8 est√°n dados por: ‚éß‚é™‚é®‚é™‚é© ak‚ÄÖ=‚ÄÖ1 ‚ÄÖpara¬Ýk‚ÄÖ=‚ÄÖ0 ‚ÄÖ ‚ÄÖ ‚ÄÖ ‚ÄÖ ak‚ÄÖ=‚ÄÖcos‚éõ‚éù(kœÄ)/(4)‚éû‚éÝ‚ÄÖ+‚ÄÖsin‚éõ‚éù(3kœÄ)/(4)‚éû‚éÝ ‚ÄÖpara¬Ýk‚ÄÖ‚âÝ‚ÄÖ0
- Grafique el espectro con los coeficientes ak.
- Obtenga la expresión para x[n] cuyo espectro es el especificado y grafique la señal.
-
Obtenga la salida y[n] para el filtro indicado. Grafique la respuesta en frecuencia del filtro. y[n]‚ÄÖ‚àí‚ÄÖ1.4542y[n‚ÄÖ‚àí‚ÄÖ1]‚ÄÖ+‚ÄÖ0.5741y[n‚ÄÖ‚àí‚ÄÖ2]‚ÄÖ=‚ÄÖ0.3x[n]‚ÄÖ+‚ÄÖ0.59x[n‚ÄÖ‚àí‚ÄÖ1]‚ÄÖ+‚ÄÖ0.03x[n‚ÄÖ‚àí‚ÄÖ2]
- Diseñe un filtro Butterwoth apropiado de manera que y[n] incluya las componentes de la 1a y 2a armónica.
-
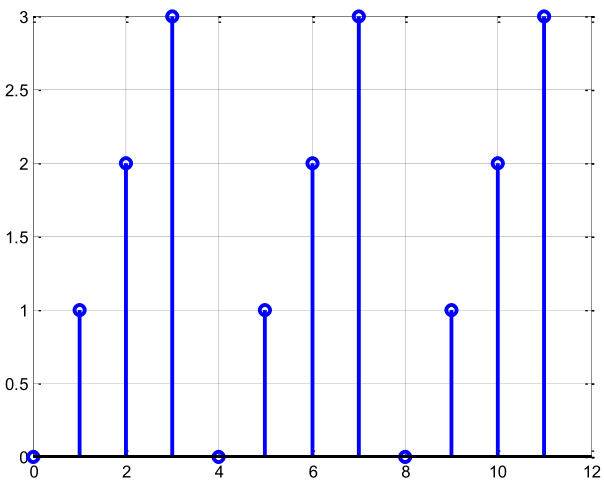
Considere la señal de TD periódica.
- Obtenga una expresión para la señal y determine el periodo.
- Mediante la ecuación de análisis, obtenga y grafique los coeficientes de la serie de Fourier.
- Obtenga y grafique la señal, mediante la ecuación de síntesis.
-
Considere las señales x[n] y x1[n].
x1[n]‚ÄÖ=‚ÄÖ‚ÄÖ‚àí‚ÄÖ0.5- Grafique m[n].
- Grafique el espectro de m[n].
- Seleccione los filtros Butterwoth apropiados de manera que y[n] = 1aarmónica y y1[n] = 5a armónica.
-
Los coeficientes espectrales de la señal x[n] son los que se indican, si el periodo de la señal es N = 10.a0 = (1)/(2) a3 = a∗ − 3 = 2       a1 = a∗ − 1 = (1)/(2) a4 = a∗ − 4 =  − j4       a2 = a∗ − 2 = (1)/(j2) a5 = a∗ − 5 = 8
- Determine la expresión de la señal x[n] como una serie de cosenos.
- Dibuje el espectro en frecuencia.
- Se desea utilizar un filtro para mantener solo la tercera armónica. Seleccione el filtro adecuado y determine la respuesta del sistema.
-
Considere el esquema del siguiente sistema:
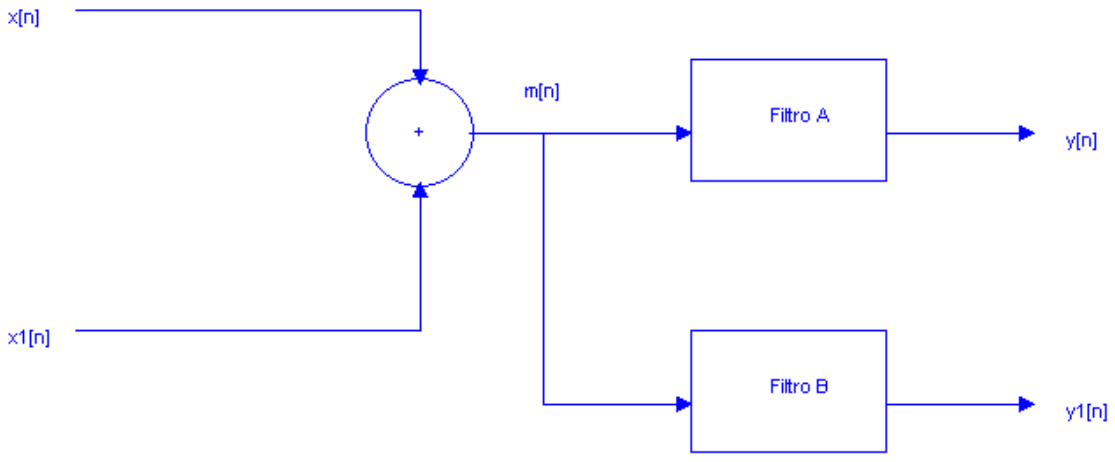 El espectro discreto y periódico con N = 6 de x[n] es como se muestra
El espectro discreto y periódico con N = 6 de x[n] es como se muestra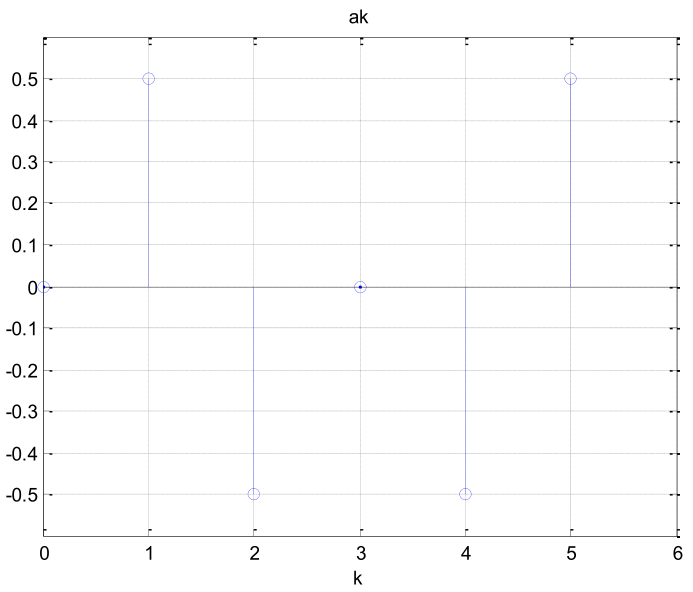 x1[n] = cos(πn)
x1[n] = cos(πn)- Obtenga x[n].
- Grafique el espectro de m[n].
-
Obtenga la salida y[n] para el filtro especificado. y[n]‚ÄÖ+‚ÄÖ1.279y[n‚ÄÖ‚àí‚ÄÖ1]‚ÄÖ+‚ÄÖ0.4776y[n‚ÄÖ‚àí‚ÄÖ2]‚ÄÖ=‚ÄÖ0.0495x[n]‚ÄÖ‚àí‚ÄÖ0.099x[n‚ÄÖ‚àí‚ÄÖ1]‚ÄÖ+‚ÄÖ0.0495x[n‚ÄÖ‚àí‚ÄÖ2]
Análisis de Fourier en TD: nivel avanzado:
-
Los coeficientes espectrales de la señal x[n] son los que se indican, si el periodo de la señal es N = 8.a0 = (1)/(2) a3 = a∗ − 3 = 2       a1 = a∗ − 1 = (1)/(2) a4 = a∗ − 4 =  − j4       a2 = a∗ − 2 = (1)/(j2) a5 = a∗ − 5 = 8
- Determine la expresión de la señal x[n] como una serie de cosenos.
- Dibuje el espectro en frecuencia.
- Se desea utilizar un filtro para mantener solo la tercera armónica. Seleccione el filtro adecuado y determine la respuesta del sistema.
-
Los coeficientes espectrales de una se√±al x[n] peri√≥dica est√°n dados por: ak‚ÄÖ=‚ÄÖsin‚éõ‚éù(kœÄ)/(3)‚éû‚éÝ 0‚Äւ⧂ÄÖk‚Äւ⧂ÄÖ6
- Grafique el espectro con los coeficientes ak.
- Obtenga y grafique x[n] cuyo espectro es el especificado.
- Seleccione los filtros Butterwoth apropiados de manera que y[n] incluya las componentes de la 1a y 2a armónica.
-
Los coeficientes espectrales de la señal x[n] son los que se indican, si el periodo de la señal es N = 6.a0 = (1)/(2) a3 = a∗ − 3 = 2       a1 = a∗ − 1 = (1)/(2) a4 = a∗ − 4 =  − j4       a2 = a∗ − 2 = (1)/(j2) a5 = a∗ − 5 = 8
- Determine la expresión de la señal x[n] como una serie de cosenos.
- Dibuje el espectro en frecuencia.
- Se desea utilizar un filtro para mantener solo la tercera armónica. Seleccione el filtro adecuado y determine la respuesta del sistema.
-
Los coeficientes espectrales de una señal x[n] periódica están dados por: k = 0,  1,  2,  3,  4,  5,  6ak = (5)/(7),  (425)/(1651),  ( − 295)/(1656),  (59)/(928),  (59)/(928),  ( − 295)/(1656),  (425)/(1651)
- Grafique el espectro con los coeficientes ak.
- Obtenga y grafique x[n] cuyo espectro es el especificado.
- Seleccione los filtros Butterwoth apropiados de manera que y[n] incluya las componentes de la 1a y 2a armónica.
-
Los coeficientes de Fourier indicados, corresponden a una señal x[n] periódica.ak = 0.7143,  0.2574,   − 0.1781,  0.0636,  0.0636,   − 0.1781,  0.2574     0.7143,  0.2574,   − 0.1781,  0.0636,  0.0636,   − 0.1781,  0.2574
- Obtenga la gr√°fica del espectro con k‚ÄÖ=‚ÄÖ0 centrada.
- Determine el periodo N de la señal.
- Obtenga la expresión de la correspondiente señal en el tiempo discreto.
- Verifique los coeficientes de la señal obtenida corresponden a los ya dados en este ejercicio.
-
Considere la siguiente se√±al discreta x[n]‚ÄÖ=‚ÄÖ1.5cos‚éõ‚éù(4œÄn)/(3)‚éû‚éÝ‚ÄÖ+‚ÄÖsin‚éõ‚éù(3œÄn)/(4)‚ÄÖ+‚ÄÖ(œÄ)/(4)‚éû‚éÝ
- Grafique el espectro con de x[n].
- A partir del espectro reconstruya la señal.
- Seleccione un filtro Butterwoth apropiado de manera que y[n] incluya solo la componente de directa.
- Seleccione los filtros Butterwoth apropiados de manera que los filtros separen cada una de las señales de la cuales se compone la entrada x[n].
-
Los coeficientes de Fourier indicados, corresponden a una señal x[n] periódica. ak = 0.6000,  0.3236,   − 0.1236,   − 0.1236,  0.3236,  0.6000,  0.3236      − 0.1236,   − 0.1236,  0.3236,  0.6000,  0.3236,   − 0.1236,   − 0.1236,  0.3236
- Obtenga la gr√°fica del espectro con k‚ÄÖ=‚ÄÖ0 centrada.
- Determine el periodo N de la señal.
- Obtenga la expresión de la correspondiente señal en el tiempo discreto.
- Verifique los coeficientes de la señal obtenida corresponden a los ya dados en este ejercicio.
-
Considere las señales x[n] cuyo espectro es el siguiente:
- A partir del espectro reconstruya la señal x[n] y grafíquela.
- A partir de la señal x[n] que obtuvo en a) obtenga el espectro y determine los coeficientes para verificar que es correcto.
- Seleccione un filtro Butterwoth apropiado y obtenga la expresión de y[n] de manera que incluya la componente de directa y la 1a armónica. Grafique la señal y[n].
-
Una se√±al x[n] peri√≥dica est√° definida como: x[n]‚ÄÖ=‚ÄÖ1 0‚Äւ⧂ÄÖn‚Äւ⧂ÄÖ4¬Ý‚ÄÖy¬Ý6‚Äւ⧂ÄÖn‚Äւ⧂ÄÖ9 ‚ÄÖ ‚ÄÖ x[n]‚ÄÖ=‚ÄÖ0 n‚ÄÖ=‚ÄÖ5y el periodo es de 10.
- Determine y grafique los coeficientes de la serie de Fourier.
- A partir de los coeficientes obtenga de nuevo la señal.
-
Una se√±al x[n] peri√≥dica est√° definida como: x[n]‚ÄÖ=‚ÄÖ1 0‚Äւ⧂ÄÖn‚Äւ⧂ÄÖ5¬Ý‚ÄÑ‚ÄÖy ‚ÄÖ ‚ÄÖ x[n]‚ÄÖ=‚ÄÖ0 6‚Äւ⧂ÄÖn‚Äւ⧂ÄÖ9y el periodo es de 10.
- Determine y grafique los coeficientes de la serie de Fourier.
- A partir de los coeficientes obtenga de nuevo la señal.
-
Considere el esquema del siguiente sistema:
 El espectro discreto y periódico con N = 6 de x[n] es como se muestra
El espectro discreto y periódico con N = 6 de x[n] es como se muestra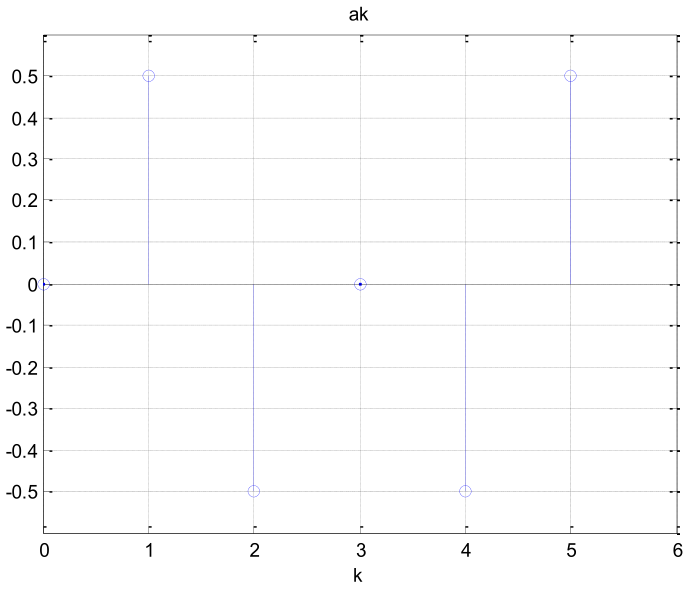 x1[n] = cos(πt)
x1[n] = cos(πt)- Obtenga x[n].
- Grafique el espectro de m[n].
-
Obtenga la salida y[n] para el filtro especificado. y[n]‚ÄÖ+‚ÄÖ1.279y[n‚ÄÖ‚àí‚ÄÖ1]‚ÄÖ+‚ÄÖ0.4776y[n‚ÄÖ‚àí‚ÄÖ2]‚ÄÖ=‚ÄÖ0.0495x[n]‚ÄÖ‚àí‚ÄÖ0.099x[n‚ÄÖ‚àí‚ÄÖ1]‚ÄÖ+‚ÄÖ0.0495x[n‚ÄÖ‚àí‚ÄÖ2]
-
Considere las señales x[n] y x1[n].

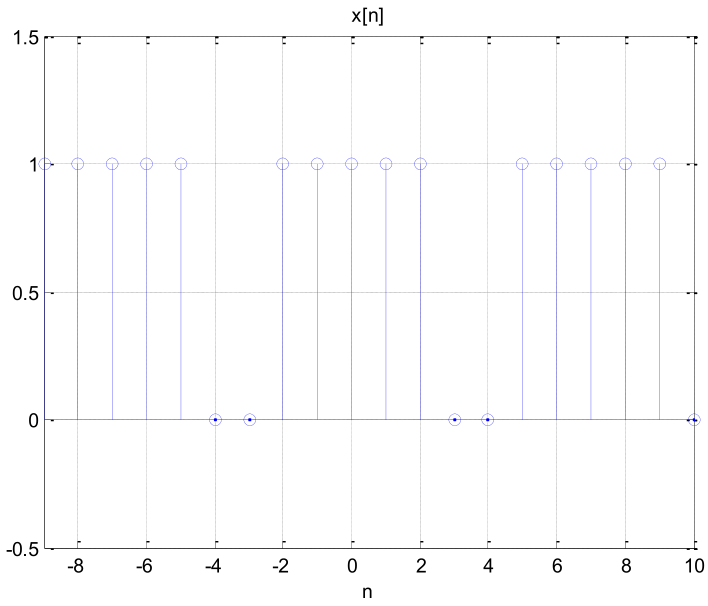 x1[n]‚ÄÖ=‚ÄÖ‚ÄÖ‚àí‚ÄÖ0.5
x1[n]‚ÄÖ=‚ÄÖ‚ÄÖ‚àí‚ÄÖ0.5- Grafique m[n].
- Grafique el espectro de m[n].
- Seleccione los filtros Butterwoth apropiados de manera que y[n] = 1a armónica y y1[n] = 5a armónica.
-
Obtenga la convolución de las señales r(t) = x[n]∗x1[n] = x1[n]∗x[n].
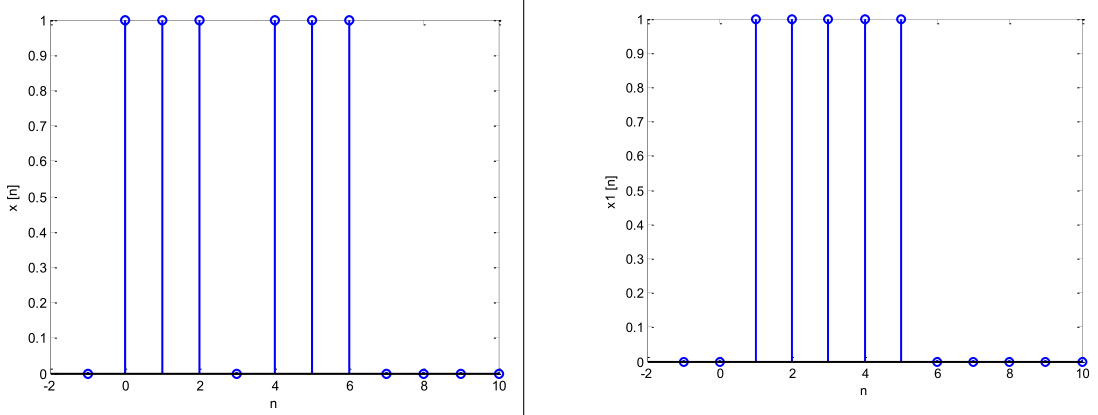
-
Los coeficientes espectrales de una se√±al x[n] peri√≥dica est√°n dados por: ak‚ÄÖ=‚ÄÖsin‚éõ‚éù(kœÄ)/(3)‚éû‚éÝ 0‚Äւ⧂ÄÖk‚Äւ⧂ÄÖ6
- Grafique el espectro con los coeficientes ak.
- Obtenga y grafique x[n] cuyo espectro es el especificado.
- Seleccione los filtros Butterwoth apropiados de manera que y[n] incluya las componentes de la 1a y 2a armónica.