Selecciona una opciĂłn para visualizarla
Video tutoriales dirigidos a:
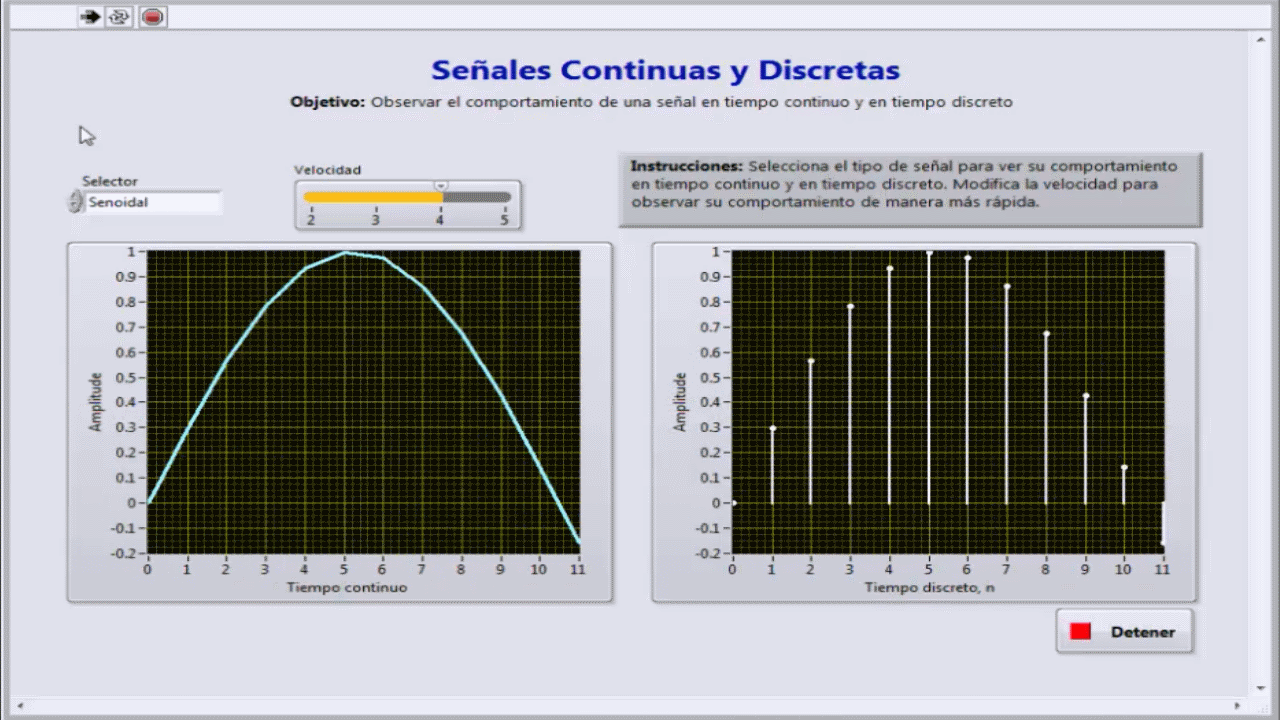
- La generación de señales en tiempo continuo y en tiempo discreto
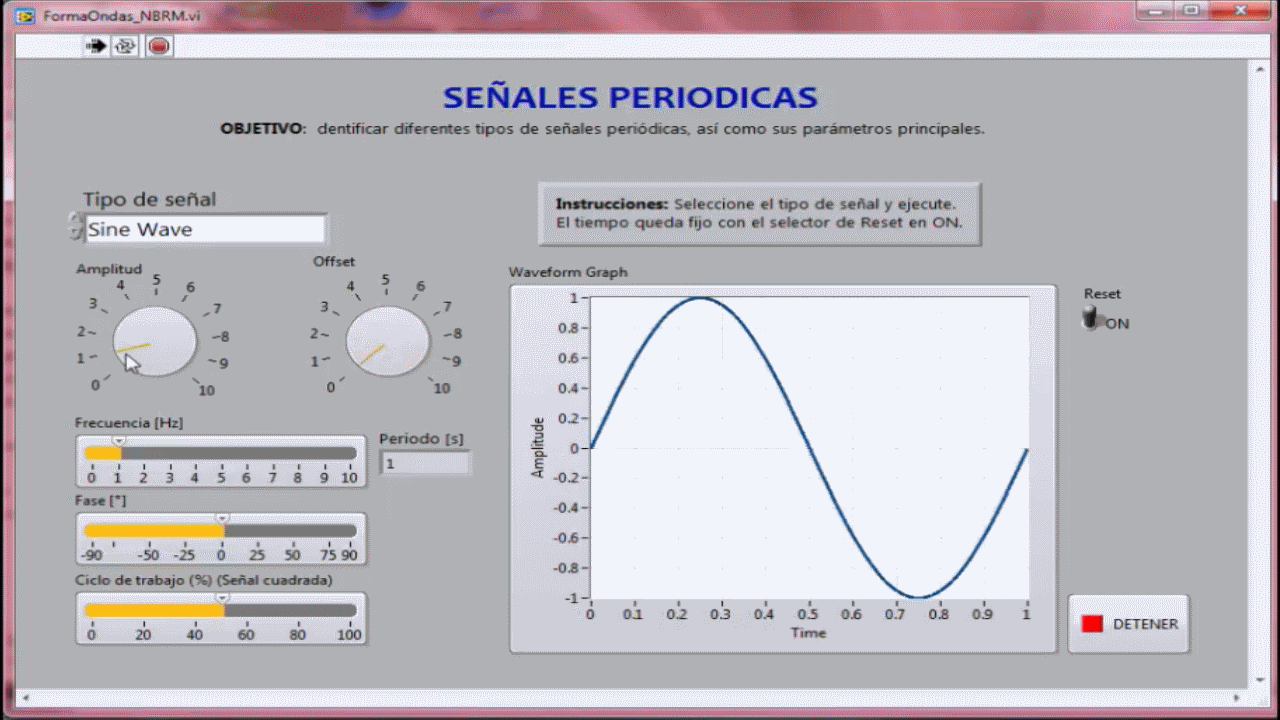
- Señales periódicas y sus parámetros
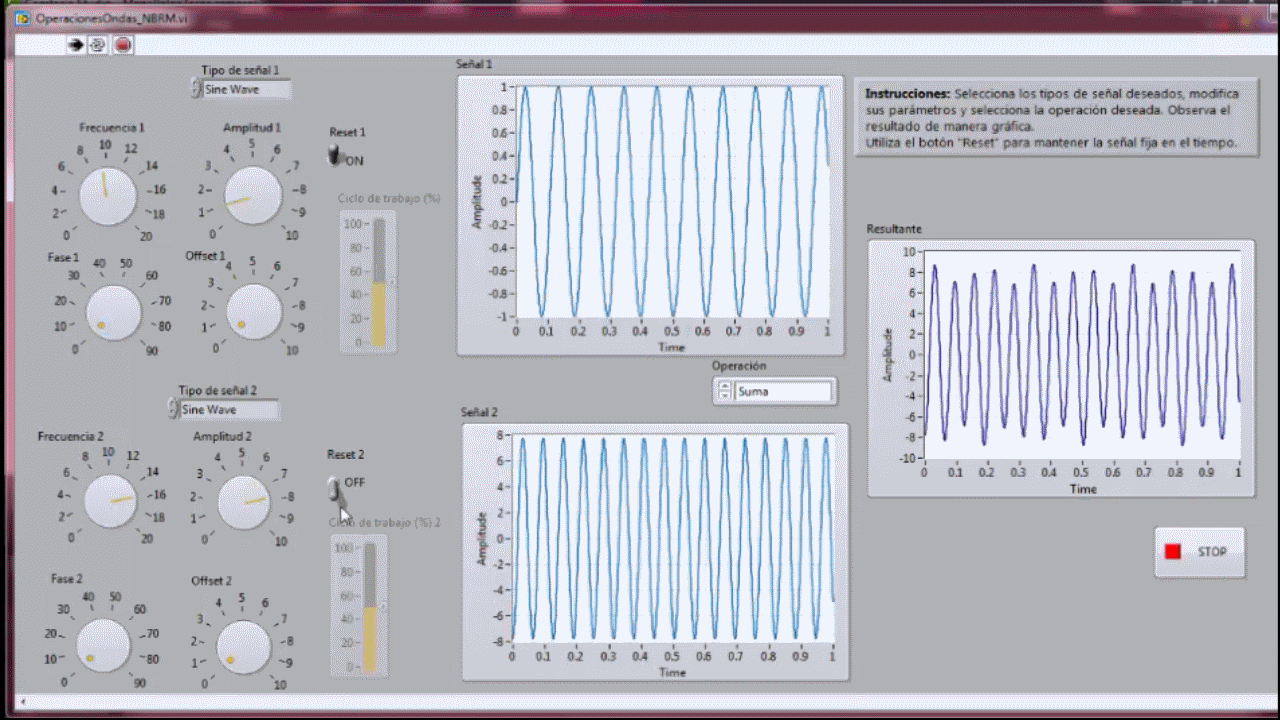
- Operaciones de Señales
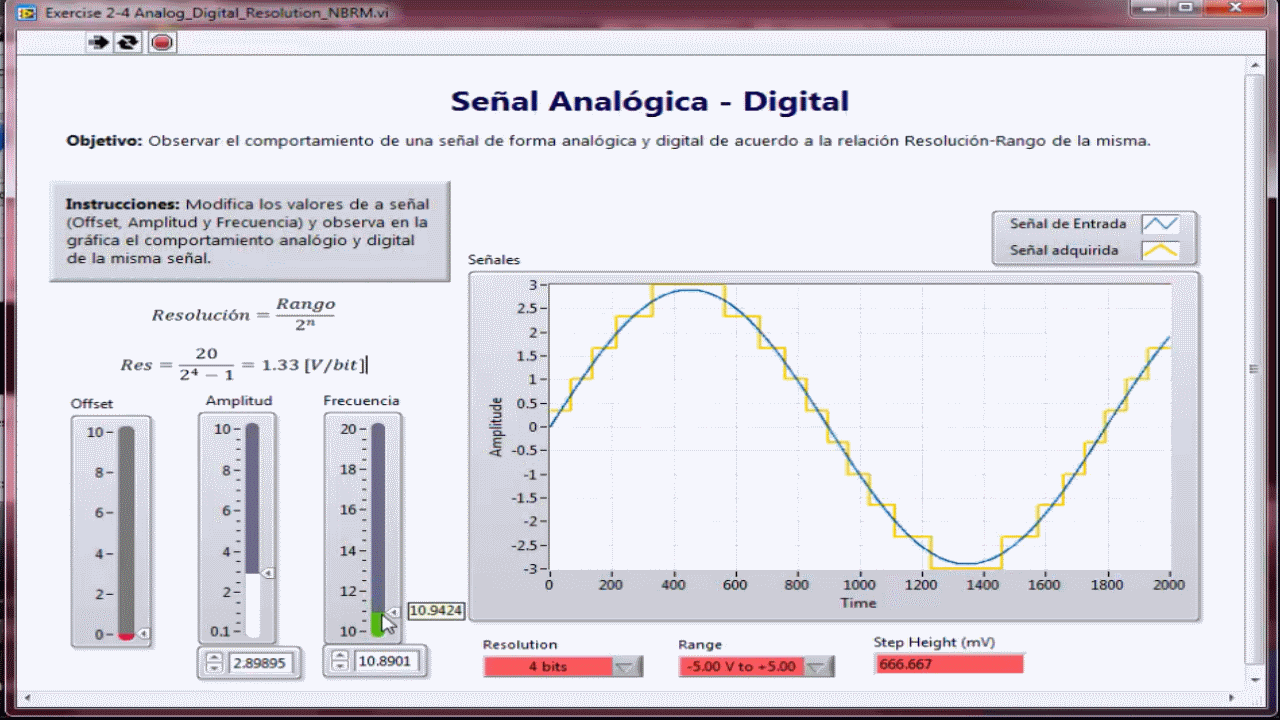
- Muestreo de señal analógica
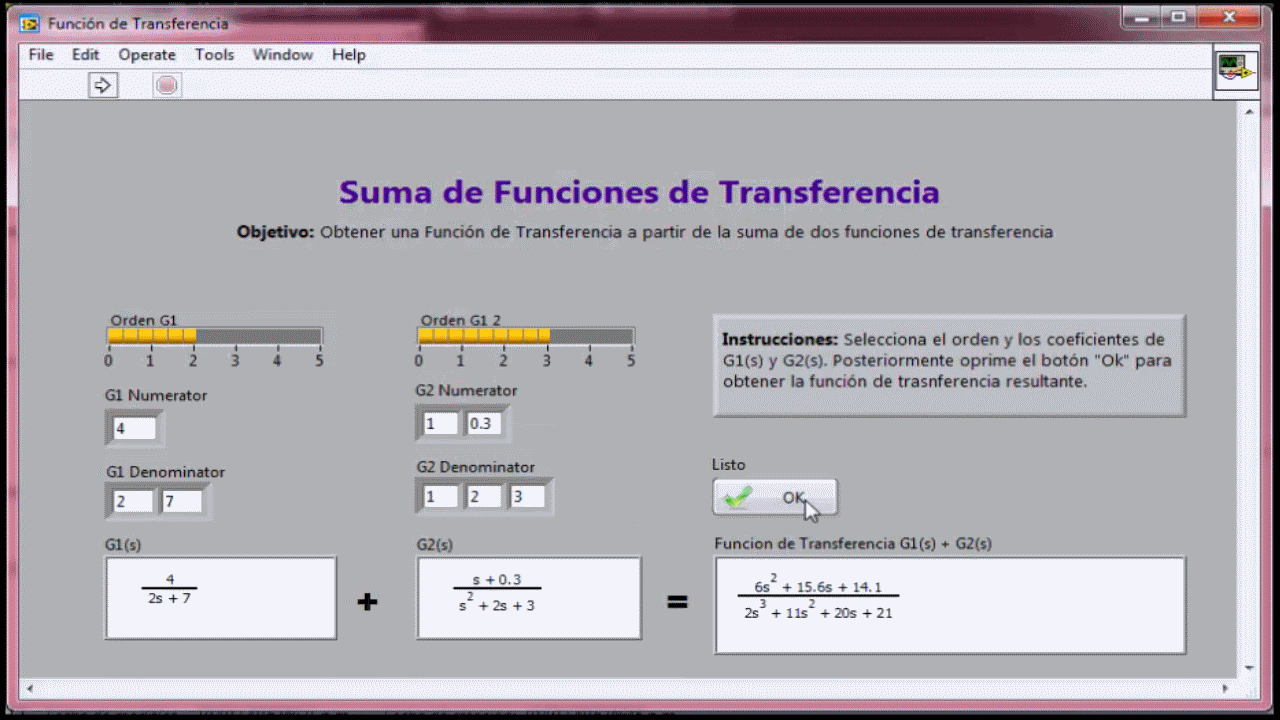
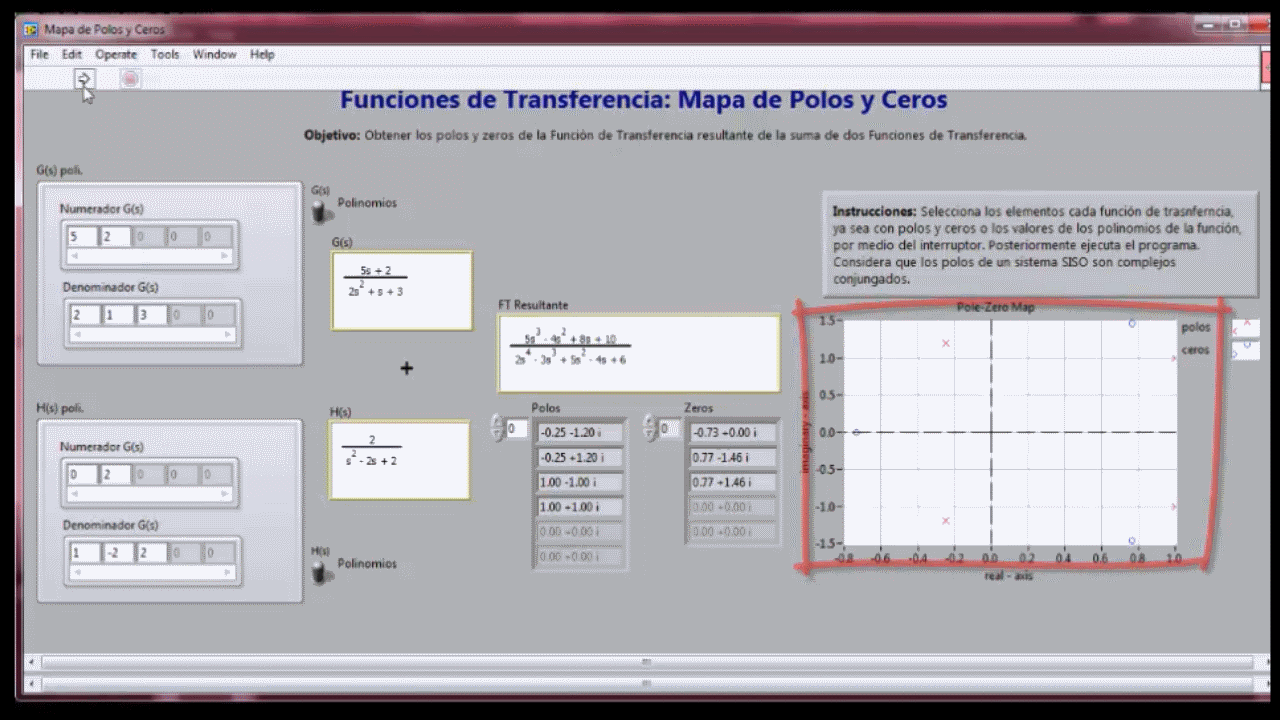
- ConexiĂłn en paralelo de Sistemas: FunciĂłn de transferencia
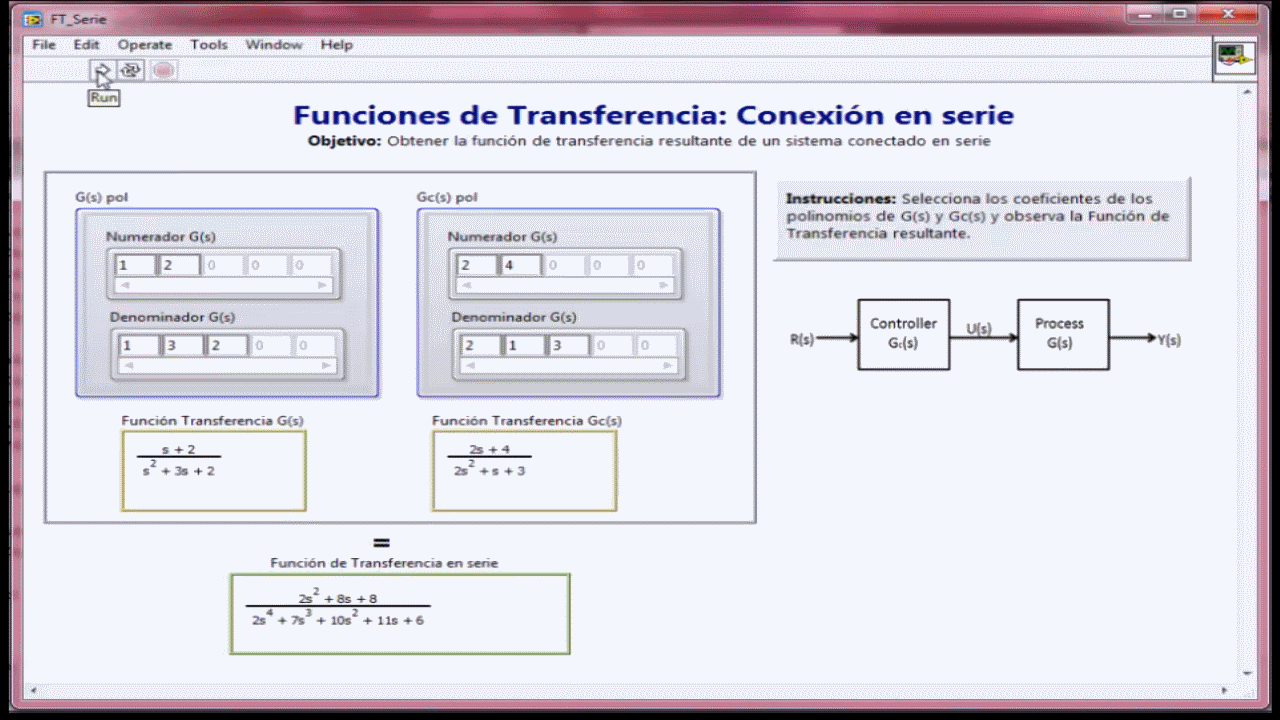
- ConexiĂłn en cascada de Sistemas: FunciĂłn de transferencia
- Diagrama de polos y ceros en TC
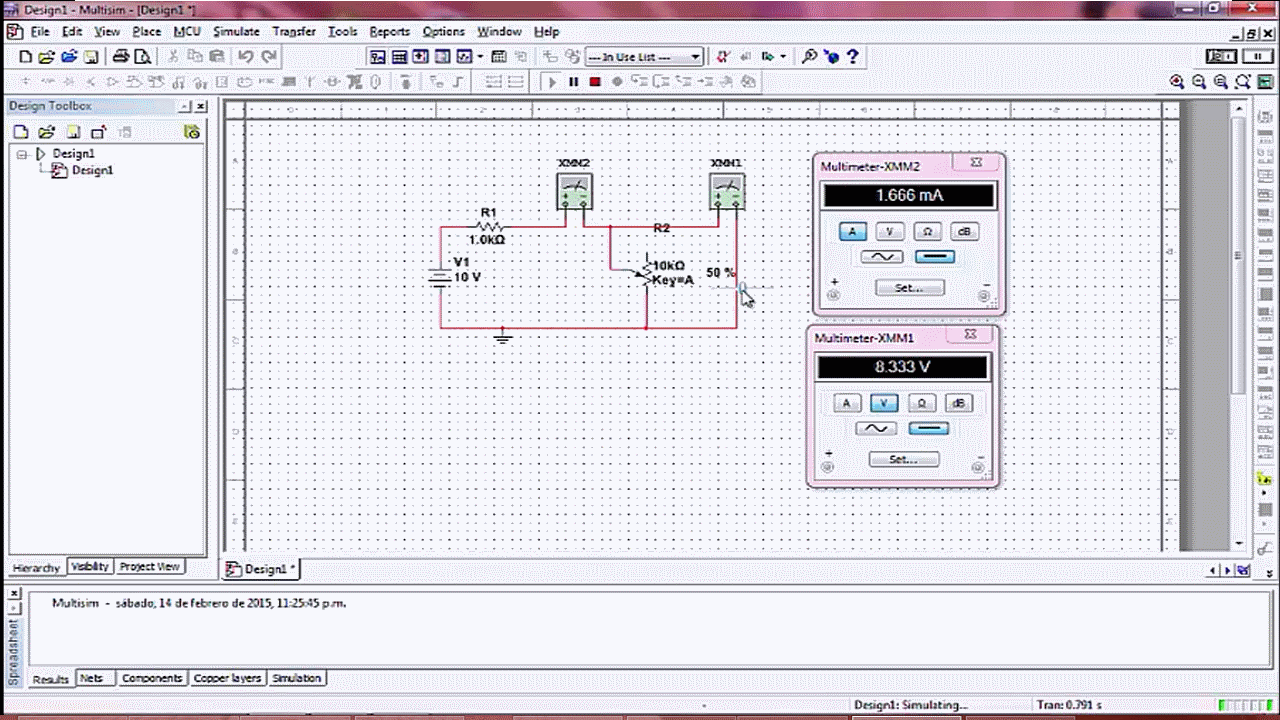
- Tutorial de Multisim
Elige el tema del video que quiera visualizar
CĂłdigos de MatLab
Una herramienta muy poderosa para el análisis de señales y sistemas es Matlab. En esta sección se presentan los códigos de funciones y programas principales utilizados en diversos ejercicios de este material.
Puedes seleccionar y copiar el código que necesites para la función mencionada.
EscalĂłn Unitario TC
%Escalon Unitario TC %FunciĂłn escalon function u = us(t) u = + 1.*(t>=0);
Rampa de TC
%Rampa de TC function r=rs(t) r=0.*(t<0)+t.*(t>0);
Señal exponencia de TC
%Senal exponencial de TC real variando c y a, t es el tiempo function [t,x]=exporeal(t,c,a) x=c*exp(a*t);
Señal arbitraria de TC
%Señal arbitraria de TC function x1=x1t(t) %Funcion x1(t) x1=us(t+1)-rs(t+1)+2*rs(t)-rs(t-2)-2*us(t-2);
Muestra discreta
%Muestra discreta function u=dd(n) %muestra discreta u=1*(n==0);
EscalĂłn Unitario TD
%Escalon Unitario TD function x=ud(n) x=1.*(n>=0);
Rampa en TD
%Rampa en TD function r=rd(n) %Rampa en TD r=0.*(n<0)+n.*(n>=0 & (n-fix(n)==0));
Señal arbitraria en TD
%Senal arbitraria en TD function xd1=xd11(n)%funciĂłn xd xd1=ud(n+2)+rd(n)-rd(n-3)-4*ud(n-4);
Respuesta al impulso de sistema TC
%Respuesta de sistema TC. ExpanciĂłn en fracciones parciales a=[1 7 10];b=6; [r p k]=residue(b,a)
Respuesta al impulso. Sistema 2o orden TD
%Respuesta al impulso. Sistema 2o orden function sis2d(b,a) %a=conv([1 1+j],[1 1-j]) Forma en que se da a y b zplane(b,a) [r p k]=residuez(b,a) n=[0:5]’; h=impz(b,a,n); h1=r(1).*(p(1).^n)+r(2).*(p(2).^n); sys = tf([0 0 1],[1 0 1],1,’Variable’,’z^-1’) [abs(r(1)) angle(r(1))*180/pi abs(p(1)) angle(p(1))*180/pi;... abs(r(2)) angle(r(2))*180/pi abs(p(2)) angle(p(2))*180/pi] [n h h1]
Sistema TD Respuesta al impulso
%Sistema TD Respuesta al impulso function sis2d(b,a) %a=conv([1 1+j],[1 1-j]) Ejemplo de a %Diagrama de polos y ceros zplane(b,a) [r p k]=residuez(b,a) n=[0:5]’; %Respuesta al impulso h=impz(b,a,n); h1=r(1).*(p(1).^n)+r(2).*(p(2).^n); %Función del sistema sys = tf([0 0 1],[1 0 1],1,’Variable’,’z^-1’) [abs(r(1)) angle(r(1))*180/pi abs(p(1)) angle(p(1))*180/pi;... abs(r(2)) angle(r(2))*180/pi abs(p(2)) angle(p(2))*180/pi] %Respuesta al impulso [n h h1]
ConvoluciĂłn en TD
%ConvoluciĂłn en TD, nx es vector de TD, x es vector de entrada function [ny y]=convd(nx,x,nh,h) ny=nx(1)+nh(1)+(0:(length(nx)+length(nh)-2)); y=conv(x,h); stem(ny,y)
Respuesta de Sistema de TD
%Respuesta de Sistema de TD function x=ejeZ(b,a) %a=[1 -2.5 1]; %b=[2 -2.5]; [r,p,k] = residuez(b,a) n=0:5; %Respuesta al impulso h=impz(b,a,n) stem(n,h); grid; zplane(b,a) a1=conv(a,[1 -1]); %ExpansiĂłn en fracciones parciales a entrada escalĂn [r,p,k] = residuez(b,a1) n=0:5; %Respuesta al escalĂłn s1=impz(b,a1,n) stem(n,s1); grid;
Transformada Z RaĂces
% Transformada Z %RAICES DIFERENTES a=[1 -2.5 1] b=[2 -2.5] roots(a) roots(b) zplane(b,a) [R,P,K] = RESIDUEZ(b,a) ​ %RAICES IGUALES a=[1 -3/2 1/2] b=[0 0 0 1/2] zplane(b,a) [R,P,K] = RESIDUEZ(b,a) ​ %RAICES REPETIDAS REALES a=[1 -5 8 -4] b=[0 3 -1] zplane(b,a) [R,P,K] = RESIDUEZ(b,a) ​ %RAICES COMPLEJAS a=[1 -2 1.5 -.5] b=[2 1.5] zplane(b,a) [R,P,K] = RESIDUEZ(b,a)
Filtro Butter Paso Bajas TC
%Filtro Butter Paso Bajas TC t=0:.0001:10-.0001; wo=2*pi; x=cos(wo*t)+0.1.*cos(25*wo*t); %señal que se desea filtrar ​ subplot(221),plot(t,x);grid; title(’x=cos(wo*t)+0.1.*cos(25*wo*t)’); %grà fica de la señal ​ %se define una frecuencia de corte que permite pasar la señal deseada %y mediante un modelo de 4° orden se elimina la vigèsima quinta armònica wc=12*pi; %frecuencia de corte [b,a]=butter(4,wc,’s’); %filtro butter obtiene los coeficientes de la %funcion de transferencia [H,wc]=freqs(b,a); %obtiene la respuesta en frecuencia ​ subplot(222),plot(wc,abs(H));grid; %grà fica de la respuesta en frecuencia title(’Filtro : |H(jw)|’); %respuesta a cualquier entrada, en este caso se elmina 0.1.*cos(25*wo*t) y=lsim(b,a,x,t); ​ %gráfica de la señal original ya filtrada; es decir, y(t) subplot(224),plot(t,y);grid; title(’Despuès del filtro: y=cos(wo*t)=cos(2*pi*t)’); ​ %gráfica de la respuesta en frecuencia subplot(223),plot(wc,angle(H)*180/pi);grid; title(’Filtro : angle H(jw)’);
Coeficientes ak de señal en TD
%Coeficientes ak de señal en TD n=0:5; x1=cos(pi*n/3)-cos(2*pi*n/3); ak=(1/length(n)).*fft(x1); stem(n,real(ak)) axis([-1 6 -1 1]) grid ​
Filtro digital Paso Banda
%Filtro digital Paso Banda [b,a]=butter(2,[.2 .3]); [H,w]=freqz(b,a); plot(w,abs(H)) grid
Filtro TC Paso Baja
%Filtro TC Paso Baja [b,a]=butter(2,10,’s’) [H,w]=freqs(b,a); plot(w,abs(H)) grid
Ejecutables de MatLab
En esta secciĂłn se presentan ejercicios de autoevaluaciĂłn ejecutables, que el estudiante puede descargar. Se incluye el procedimiento para la instalaciĂłn.
Selecciona un ejecutable y pulsa en Ă©l para descargarlo. Recuerda que debes tener instalado el RunTime de Matlab para poderlo abrir, si no sabes como hacerlo puedes descargar el primer ejecutable junto con el mencionado RunTime dando click aquí y seguir el tutorial que aparecerá dando click aquí.
Ejecutables de LabView
En esta secciĂłn se presentan ejercicios ejecutables que puede descarga, para que el estudiante pueda ejercitarse en la comprensiĂłn de diversos temas con respuesta en tiempo real. Se incluye el procedimiento para la instalaciĂłn.
Selecciona un ejecutable y pulsa en Ă©l para descargarlo. Recuerda que debes tener instalado el Run-time Engine 2012 para poderlo abrir, si no sabes como hacerlo puedes seguir el tutorial descargando el archivo dando click aquí.