- Sistemas TC y TD
- SeΓ±ales TC y TD
- SLIT TC
- SLIT TD
- Fourier TC
- Fourier TD
Selecciona un tema de arriba.
Primero selecciona un tema de arriba.
Señales en TC y en TD:
En los ejemplos con soluciΓ³n de esta secciΓ³n se abordan conceptos de seΓ±ales continuas y discretas. Se realizan operaciones y transformaciones de las seΓ±ales. Se presentan seΓ±ales fundamentales de tiempo continuo y discreto y su representaciΓ³n en el dominio del tiempo. Se presenta el anΓ‘lisis de seΓ±ales tanto teΓ³rico como simulado.
Selecciona la dificultad en las caritas de la izquierda.
Señales en TC y en TD nivel principiante:
- Con base en la EcuaciΓ³n 2.8, grafique la seΓ±al escalΓ³n unitario u(t).
- Con base en la EcuaciΓ³n 2.9, grafique la seΓ±al rampa r(t).
- Utilice la funciΓ³n sinc(t) para obtener la grΓ‘fica de la seΓ±al Sinc EcuaciΓ³n 2.13.
-
Utilice la funciΓ³n diric(t,N) para obtener cuatro grΓ‘ficas de la seΓ±al Dirichlet EcuaciΓ³n 2.15. Considere los siguientes valores de N: 4, 5, 7 y 8. Utilice una funciΓ³n subplot() para graficar las cuatro seΓ±ales.
(2.15) drcl(t,β N)β =β (sen(ΟNt))/(Nsen(Οt))
- Considere la seΓ±al exponencial, EcuaciΓ³n 2.16, con Cβ =β 1 y rβ =β β ββ 0.5, rβ =β 0.5, rβ =β 0. Utilice la funciΓ³n subplot() para graficar las tres seΓ±ales exponenciales.
- Considere la seΓ±al exponencial, EcuaciΓ³n 2.16, con Cβ =β 1 y rβ =β j2Ο, rβ =β β ββ 0.5β +β j2Ο, rβ =β 0.5β +β j2Ο. Utilice la funciΓ³n subplot() para graficar las tres seΓ±ales exponenciales complejas. Ya que las seΓ±ales son complejas, se tiene que graficar la parte real y la parte imaginaria, o bien la magnitud y la fase.
1)
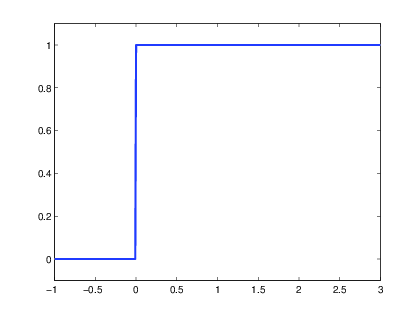
>> t=-1:0.01:3;
>> u = 0.*(t<0)+ 1.*(t>=0);
>> plot(t,u, βLineWidthβ,2)
>> axis([-1 3 -.1 1.1]);
2)
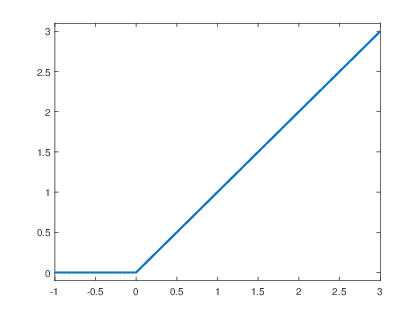
>> t=-1:0.001:3;
>> r = 0.*(t<0)+ t.*(t>=0);
>> plot(t,r, βLineWidthβ,2)
>> axis([-1 3 -.1 3.1]);
3)
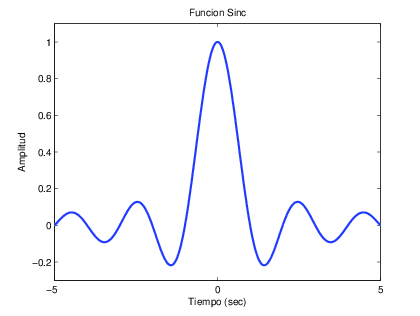
>> t = -5:.01:5;
>> y = sinc(t);
>> plot(t,y, βLinewidthβ,2);
>> xlabel(βTiempo (sec)β);ylabel(βAmplitudβ); title(βFuncion Sincβ)
>> axis([-5 5 -.3 1.1]);
La seΓ±al cruza en cero en mΓΊltiplos de mΟ y el Γ‘rea bajo la curva estΓ‘ dada por
4) La funciΓ³n para generarla en Matlab es
de manera que para obtener la seΓ±al EcuaciΓ³n 2.27 cambia a:
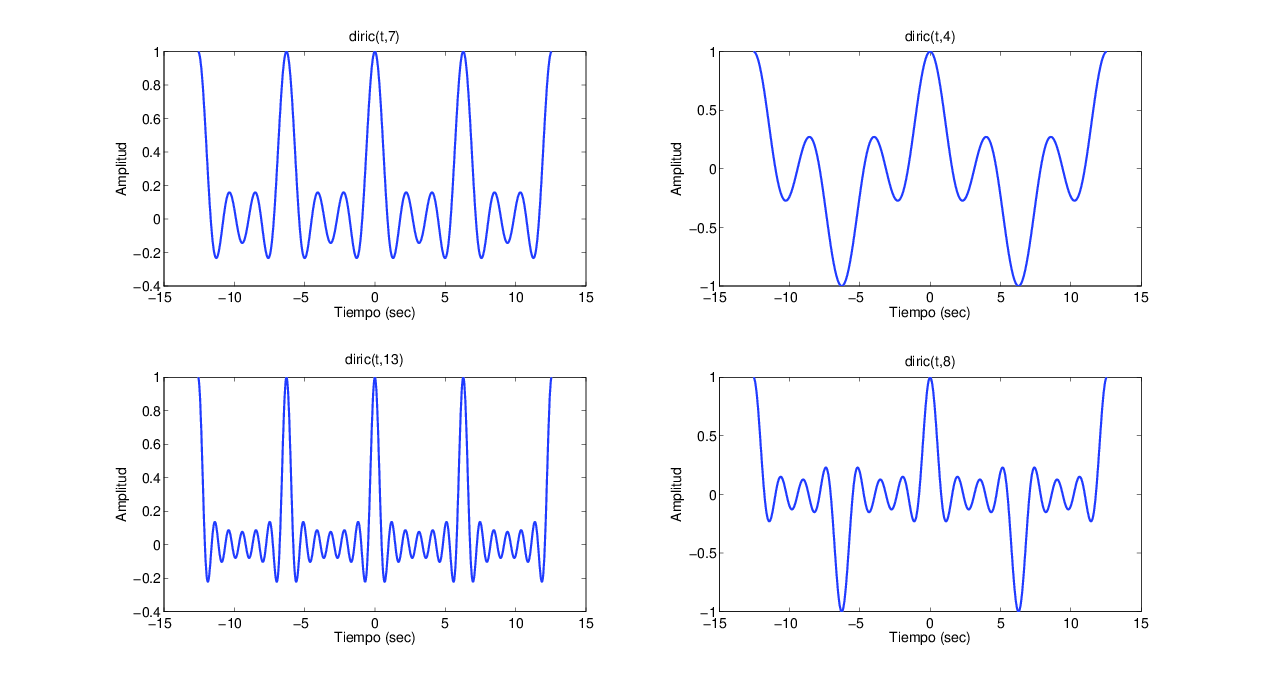
>> t = linspace(-4*pi,4*pi,1000);
>> subplot(221),plot(t,diric(t,7),βLinewidthβ,2);
>> xlabel(βTiempo (sec)β);ylabel(βAmplitudβ); title(βdiric(t,7)β)
>> subplot(222),plot(t,diric(t,4),βLinewidthβ,2);
>> xlabel(βTiempo (sec)β);ylabel(βAmplitudβ); title(βdiric(t,4)β)
>> subplot(223),plot(t,diric(t,13),βLinewidthβ,2);
>> xlabel(βTiempo (sec)β);ylabel(βAmplitudβ); title(βdiric(t,13)β)
>> subplot(224),plot(t,diric(t,8),βLinewidthβ,2);
>> xlabel(βTiempo (sec)β);ylabel(βAmplitudβ); title(βdiric(t,8)β)
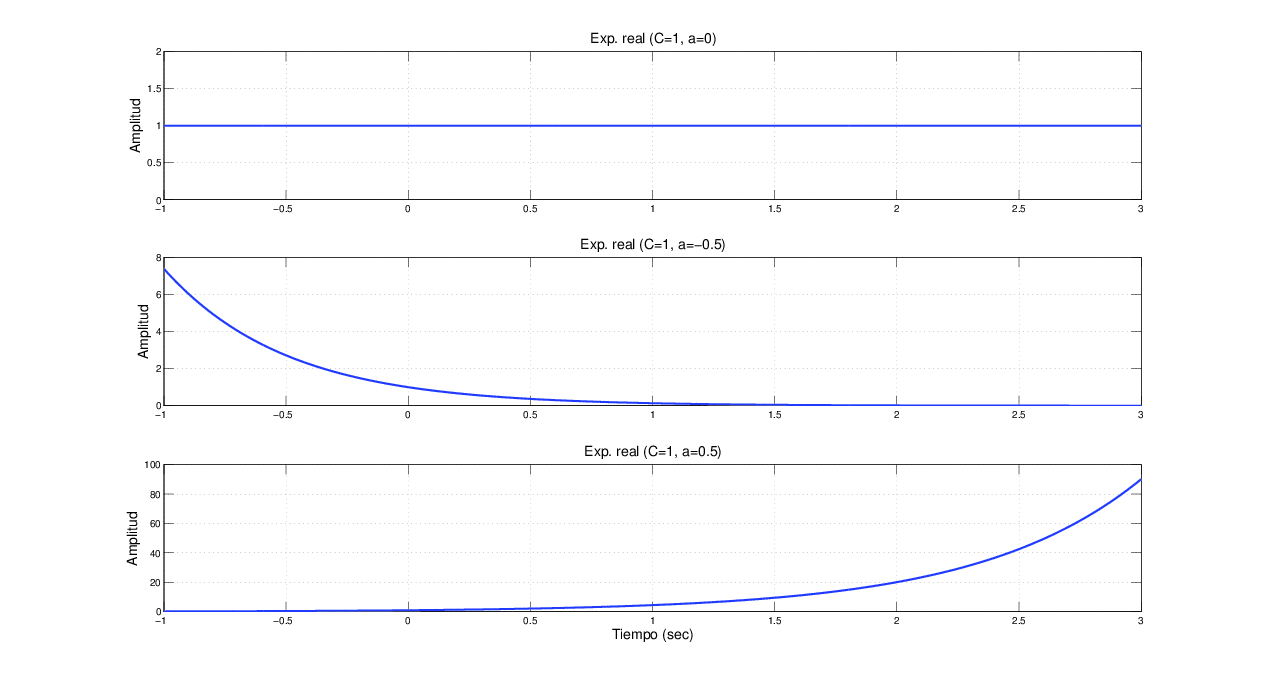
%exporeal1.m
t = linspace(-1,3,1000);
%Exponencial Real constante
c=1; r=0;
x=c*exp(r*t);
subplot(311),plot(t,abs(x),βLinewidthβ,2); grid
xlabel(βTiempo (sec)β);ylabel(βAmplitudβ);
title(βReal(Exp.real) (C=1, a=0)β)
%Exponencial Real decreciente
c=1; r=-2;
x=c*exp(r*t);
subplot(312),plot(t,abs(x),βLinewidthβ,2);grid
xlabel(βTiempo (sec)β);ylabel(βAmplitudβ);
title(βReal(Exp.real) (C=1, a=-0.5)β)
%Exponencial Real creciente
c=1; r=1.5;
x=c*exp(r*t);
subplot(313),plot(t,abs(x),βLinewidthβ,2);grid
xlabel(βTiempo (sec)β);ylabel(βAmplitudβ);
title(βReal(Exp.real) (C=1, a=0.5)β)
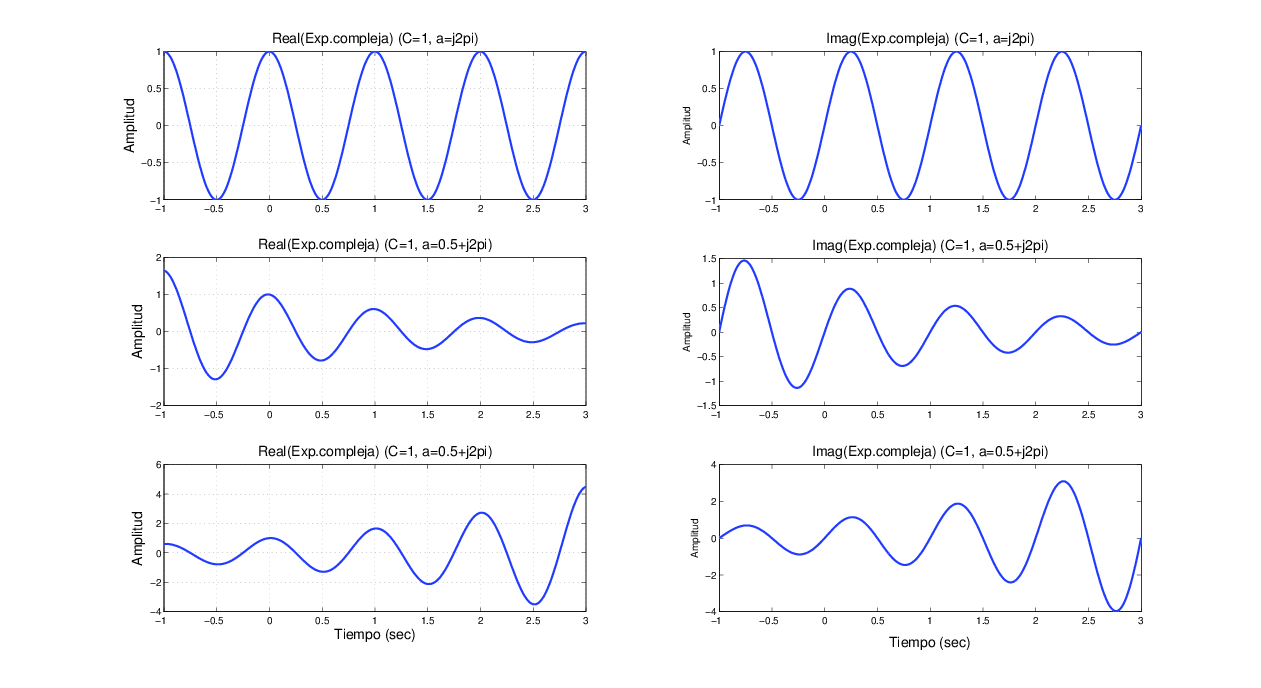
t = linspace(-1,3,1000);
%Exponencial Compleja constante
c=1; r=j*2*pi;
x=c*exp(r*t);
subplot(321),plot(t,real(x),βLinewidthβ,2); grid
xlabel(βTiempo (sec)β);ylabel(βAmplitudβ);
title(βReal(Exp.compleja) (C=1, a=j2pi)β)
subplot(322),plot(t,imag(x),βLinewidthβ,2);
xlabel(βTiempo (sec)β);ylabel(βAmplitudβ);
title(βImag(Exp.compleja) (C=1, a=j2pi)β)
%Exponencial Compleja decreciente
c=1; r=-0.5+j*2*pi;
x=c*exp(r*t);
subplot(323),plot(t,real(x),βLinewidthβ,2);grid
xlabel(βTiempo (sec)β);ylabel(βAmplitudβ);
title(βReal(Exp.compleja) (C=1, a=0.5+j2pi)β)
subplot(324),plot(t,imag(x),βLinewidthβ,2);
xlabel(βTiempo (sec)β);ylabel(βAmplitudβ);
title(βImag(Exp.compleja) (C=1, a=0.5+j2pi)β)
%Exponencial Compleja creciente
c=1; r=0.5+j*2*pi;
x=c*exp(r*t);
subplot(325),plot(t,real(x),βLinewidthβ,2); grid
xlabel(βTiempo (sec)β);ylabel(βAmplitudβ);
title(βReal(Exp.compleja) (C=1, a=0.5+j2pi)β)
subplot(326),plot(t,imag(x),βLinewidthβ,2);
xlabel(βTiempo (sec)β);ylabel(βAmplitudβ);
title(βImag(Exp.compleja) (C=1, a=0.5+j2pi)β)
SoluciΓ³n
%FunciΓ³n escalon
function u = us(t)
u = + 1.*(t>=0);
t=-1:0.01:5;
plot(t,us(t),βLinewidthβ,2); grid
SoluciΓ³n
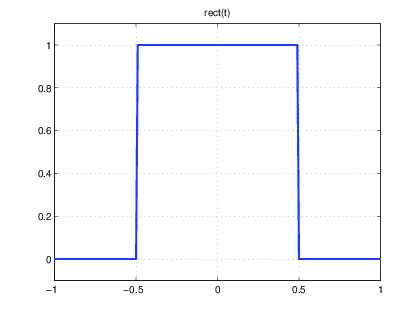
function x=rect(t)
x=1.*(abs(t)<.5);
t=-1:0.01:1;
plot(t,rect(t),βLinewidthβ,2); grid
Señales en TC y en TD nivel intermedio:
Verifique que conforme el escalamiento, en amplitud y tiempo, se incrementan, la seΓ±al tiende a las caracterΓsticas ideales del impulso unitario. Grafique en el intervalo β ββ 1β β€β tβ β€β 1.
SoluciΓ³n
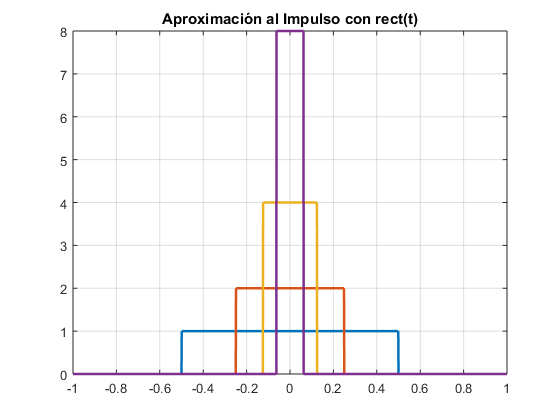
t=-1:0.001:1;
plot(t,rect(t),t,2*rect(2*t),t,4*rect(4*t),t,8*rect(8*t),βLinewidthβ,2);
grid
title(βAproximaciΓ³n al Impulso con rect(t)β)
Defina una funciΓ³n ud(n) que evalΓΊe la secuencia escalΓ³n unitario u[n], EcuaciΓ³n 1.18, cuyo parΓ‘metro de entrada sea el vector de tiempo discreto n. Con la funciΓ³n definida, grafique la seΓ±al en el intervalo β ββ 2β β€β nβ β€β 6.
SoluciΓ³n
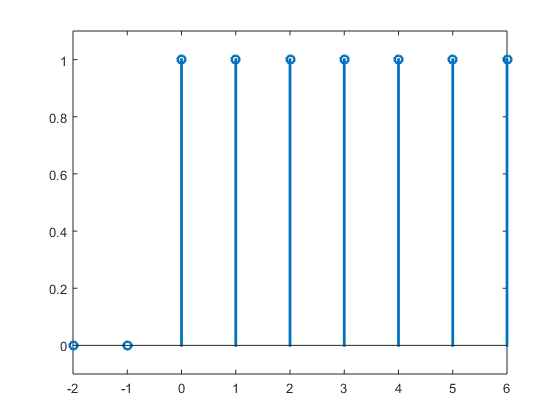
function x=ud(n)
x=1.*(n>=0);
n=-2:6;
stem(n,ud(n),βLinewidthβ,2)
SoluciΓ³n
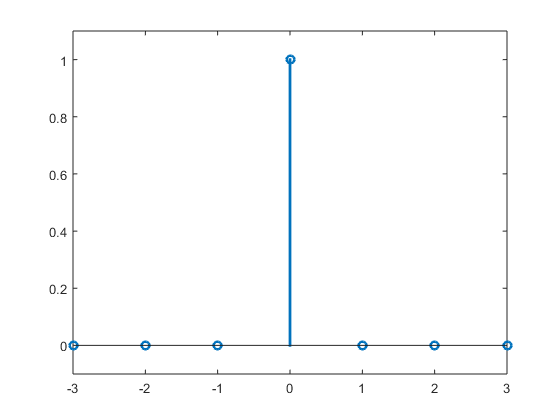
function u=dd(n) %muestra discreta
u=1*(n==0);
n=-3:3;
stem(n,dd(n),βLinewidthβ,2)
Señales en TC y en TD nivel avanzado:
SoluciΓ³n
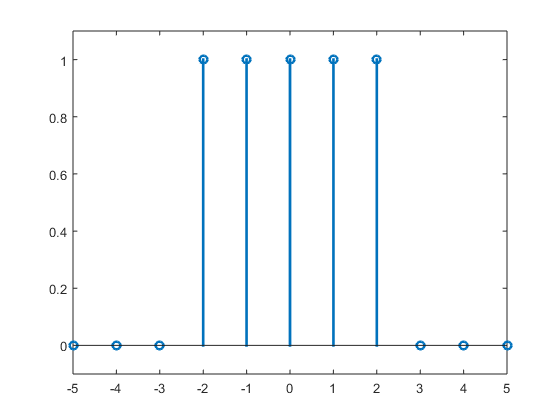
function r=rectd(n,Nw)
r=ud(n+Nw)-ud(n-Nw-1);
n=-5:5;
stem(n,rectd(n,2),βLinewidthβ,2)
SoluciΓ³n
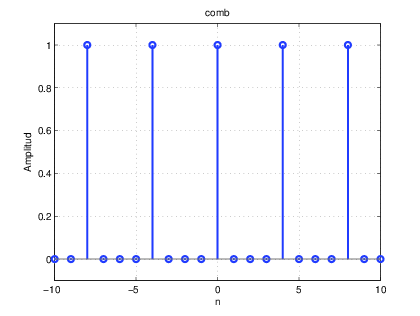
% trend.m
n=-10:10;
i=0;
iu=0;
for i = n;
iu=iu+dd(n-(4.*i));
end;
stem(n,iu,βLineWidthβ,2);axis([-10 10 -0.1 1.1]);
grid;xlabel(βnβ);ylabel(βAmplitudβ),title(βTren de impulsos discretosβ)
SoluciΓ³n
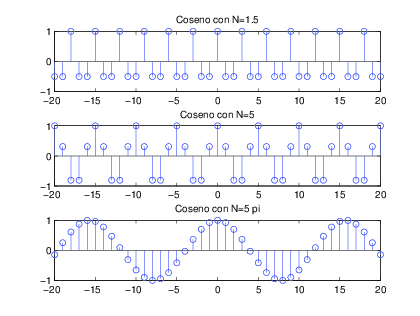
%expo1.m
n=-20:20;
N=[1.5 5 5*pi];
x1=exp(j*2*pi*n/N(1));
x2=exp(j*2*pi*n/N(2));
x3=exp(j*2*pi*n/N(3));
subplot(311),stem(n,real(x1)); title(βCoseno con N=1.5β)
subplot(312),stem(n,real(x2)); title(βCoseno con N=5β)
subplot(313),stem(n,real(x3)); title(βCoseno con N=5 piβ)
Se observa en la primera grΓ‘fica que con Nβ =β 1.5 la seΓ±al coseno es periodica, sin embargo, el periodo es Nβ =β 3, esto es debido a que N debe ser entero. Es decir, el periodo se obtiene como
En la segunda grΓ‘fica el coseno es periΓ³dico con Nβ =β 5, es decir, que con mβ =β 1, Nβ =β 5.
En la tercera grΓ‘fica se observa que el coseno es una seΓ±al aperiΓ³dica, ya que no existe m entero con el que se obtiene el mΓnimo N entero.
De lo anterior se concluye que NO todas las exponenciales complejas en tiempo discreto son perΓ³dicas.
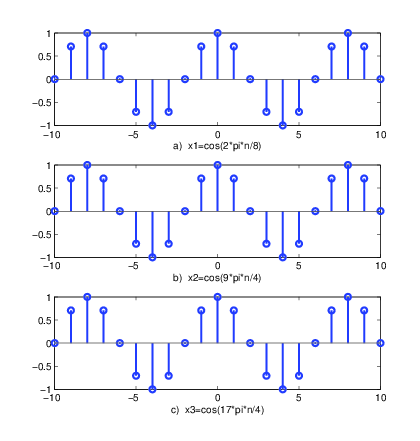
% expo2.m
n=-10:10;
x1=cos(2*pi*n/8);
x2=cos(9*pi*n/4);
x3=cos(17*pi*n/4);
subplot(311),stem(n,x1,βLineWidthβ,2); xlabel(βa) x1=cos(2*pi*n/8)β)
subplot(312),stem(n,x2,βLineWidthβ,2); xlabel(βb) x2=cos(9*pi*n/4)β)
subplot(313),stem(n,x3,βLineWidthβ,2); xlabel(βc) x3=cos(17*pi*n/4)β)
10. b)
10. c)
Sistemas:
En los ejemplos con soluciΓ³n de esta secciΓ³n se abordan conceptos de identificaciΓ³n de sistemas continuos y discretos. Se presentan las propiedades de los sistemas: linealidad, invariancia en el tiempo, causalidad y estabilidad externa.
Selecciona la dificultad en las caritas de la izquierda.
Sistemas nivel principiante:
Para los siguientes sistemas indique si el sistema es:
a) BIBOβestable
b) Causal
c) Invariante en el tiempo
d) Lineal
Ejercicio 1:
|
1)
|
y[n]
|
β
=β
|
H{x[n]}
|
|
β
=β
|
|x[n]|
|
SoluciΓ³n 1)
a) El sistema es BIBOβestable, pues el valor absoluto de una seΓ±al acotada tambiΓ©n serΓ‘ acotado.
b) El sistema es causal, pues, para cualquier valor de n, el valor absoluto de la seΓ±al de entrada evaluada en n, sΓ³lo depende de la n misma.
c) Para mostrar si el sistema es invariable, primero se obtiene la salida del sistema cuando x[n] se traslada k unidades; se denota dicha salida como yi[n]; esto es:
d) Para saber si el sistema es lineal, se utiliza la siguiente propiedad de valor absoluto: |aβ +β b|β β€β |a|β +β |b|.
Primero se define la seΓ±al yi[n] como:
Ejercicio 2:
|
2)
|
y[n]
|
β
=β
|
H{x[n]}
|
|
β
=β
|
mediana(x[nβ
ββ
1],β
x[n],β
x[nβ
+β
1]);Β aβ
β€β
nβ
β€β
b
|
Nota: en este sistema, para determinar y[a] y y[b], el sistema tendrΓa acceso a la seΓ±al de entrada en nβ =β aβ ββ 1 y en nβ =β bβ +β 1, respectivamente, por lo cual, se asume que x[nβ =β aβ ββ 1]β =β x[nβ =β a] y que x[bβ +β 1]β =β x[b].
SoluciΓ³n 2)
a) El sistema es BIBOβestable, pues la mediana de una seΓ±al acotada siempre serΓ‘ acotada.
b) El sistema es no causal, pues tiene como argumento a los valores x[nβ +β 1].
c) Para saber si el sistema es invariable, primero se obtiene la salida del sistema cuando x[n] se traslada k unidades; dicha salida se denotarΓ‘ como yi[n]; esto es:
d) Para saber si el sistema es lineal se considera que se tienen N seΓ±ales de entrada diferentes, denotadas como: xi[n], 1β β€β iβ β€β N, y que la salida para cada una de estas seΓ±ales se denota como: yi[n]; esto es:
Entonces, el sistema serΓa lineal, si y sΓ³lo si,
La ecuaciΓ³n anterior nos indica que la mediana de xi[kβ ββ 1], xi[k] y xi[kβ +β 1], para cualquier valor i, siempre tendrΓa que ser xi[kβ ββ 1]; sin embargo, dado que estas seΓ±ales xi[n] son arbitrarias, siempre serΓ‘ posible incrementar el nΓΊmero de seΓ±ales para hacer que esta condiciΓ³n no se cumpla; lo cual, lleva a concluir que el sistema es no lineal.
Sistemas nivel intermedio:
Para el sistema H que se define a continuaciΓ³n, determine grΓ‘fica y algebraicamente, si el sistema es lineal e invariante en el tiempo.
Para verificar si el sistema es invariante en n, primero se traslada a la seΓ±al de entrada x[n] en k unidades; dicha transformaciΓ³n se denota como: x[n]β ββ x[nβ ββ k]; consecuentemente: x[nβ ββ 1]β ββ x[nβ ββ 1β ββ k] y, sea yi[n] la salida del sistema para la entrada x[nβ ββ k]; esto es:
Para verificar si el sistema es lineal, primero se define el conjunto de seΓ±ales yi[n]; tales que:
Posteriormente, se hace la suma de las seΓ±ales yi[n]; esto es:
Por otra parte, se define a y0[n] como:
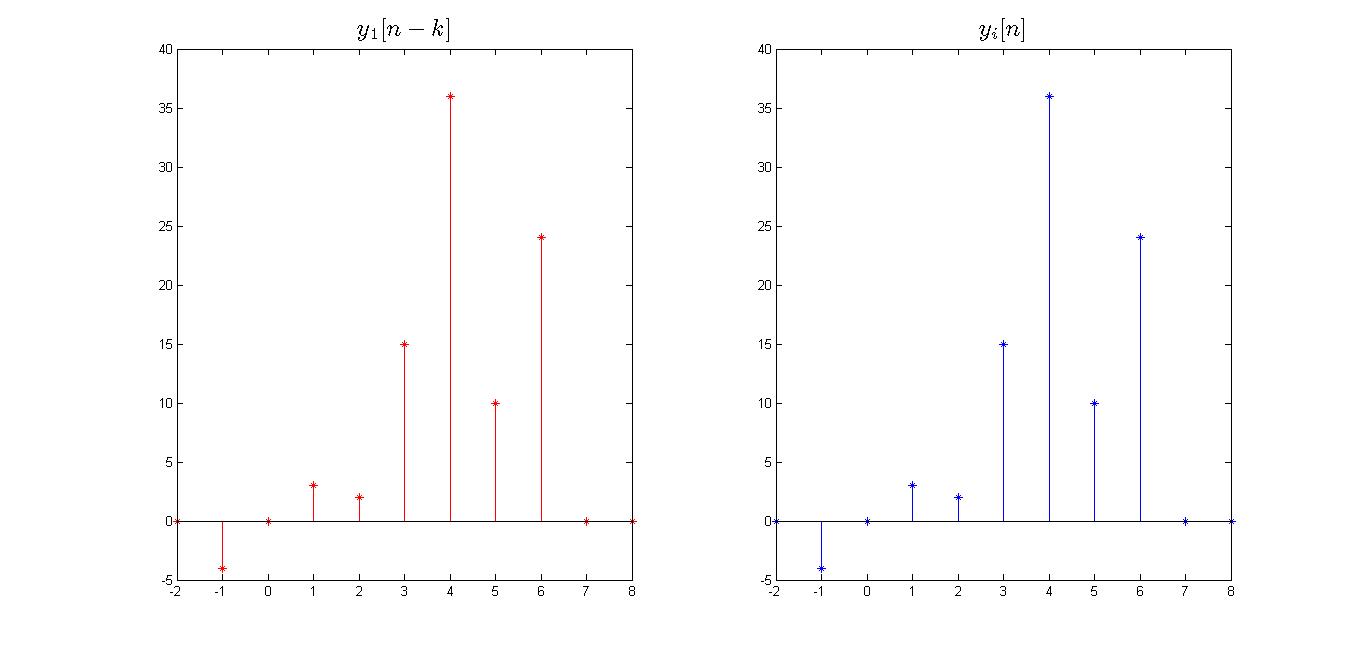
A continuaciΓ³n, se presenta una corroboraciΓ³n grΓ‘fica de los resultados obtenidos. Para resolver la parte de invariabilidad se propone el siguiente programa:
Sea y1[n] la seΓ±al de salida ante una entrada arbitraria x1[n], la cual, se propone como:
x1[n]β =β [4,β 6,β 3,β 1,β 5,β 9,β 2,β 4]; β ββ 2β β€β nβ β€β 5
nota: suponga que x1[n]β =β 0 para nβ β€β 0βͺnβ β₯β 6.
Posteriormente, se traslada la seΓ±al y1[n] kβunidades para obtener la seΓ±al y1[nβ ββ k]: Nota: en el programa que se muestra a continuaciΓ³n se propuso kβ =β β ββ 2
Paralelamente a este proceso, se obtiene la seΓ±al yi[n]; la cual, es la salida del sistema ante la seΓ±al de entrada x1[n] trasladada en kβunidades; esto es: yi[n]β =β H{x1[nβ ββ k]}.
CΓ³digo en matlab:
n=[-4,-3,-2,-1,0,1,2,3,4,5,6,7,8];
β
%--------------------------------------------%
%Definir la seΓ±al de entrada x1[n]
%n--> -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
x1=[0 0 4 6 3 1 5 9 2 4 0 0 0];
β
%--------------------------------------------%
%Obtener tamaΓ±o de la seΓ±ales x1[n]
N=length(x1);
β
%--------------------------------------------%
%Obtener y1[n]; y1[n]=(n)x1[n-1]
for ii=2:1:N
y1(ii) = (n(ii))*x1(ii-1);
end
β
%--------------------------------------------%
%Trasladar, en n, a y1[n] k-unidades;
%y1[n] --> y1[n-k]=y1_trasladada
β
%Definir k
k=-2;
%Trasladar
y1_trasladada=y1(-k+1:end);
β
%--------------------------------------------%
%obtener yi[n]; yi[n]=H{x[n-k]}=(n-k)x[n-k-1]
for ii=1:1:N+k
yi(ii) = (n(ii-k))*x1(ii-k-1);
end
β
%--------------------------------------------%
%Graficar y1[n+1] y yi[n]
β
%GrΓ‘fica de y1[n+1]
subplot(1,2,1)
stem(n(-k+1:end),y1_trasladada,β*-rβ)
β
%GrΓ‘fica de yi[n]
subplot(1,2,2)
stem(n(-k+1:end),yi,β*-β)
Para corroborar que el sistema sea lineal ante 2 seΓ±ales de entrada particulares, se propone a x1[n] y x2[n] como dichas seΓ±ales particulares de entrada; en donde:
x1[n]β =β [4,β 6,β 3,β 1,β 5,β 9,β 2,β 4]; β ββ 2β β€β nβ β€β 5
x2[n]β =β [3,β 4,β 5,β 2,β 6,β 8,β 4,β 1]; β ββ 2β β€β nβ β€β 5
nota: suponga que x1[n]β =β x2[n]β =β 0 para nβ β€β 0βͺnβ β₯β 6.
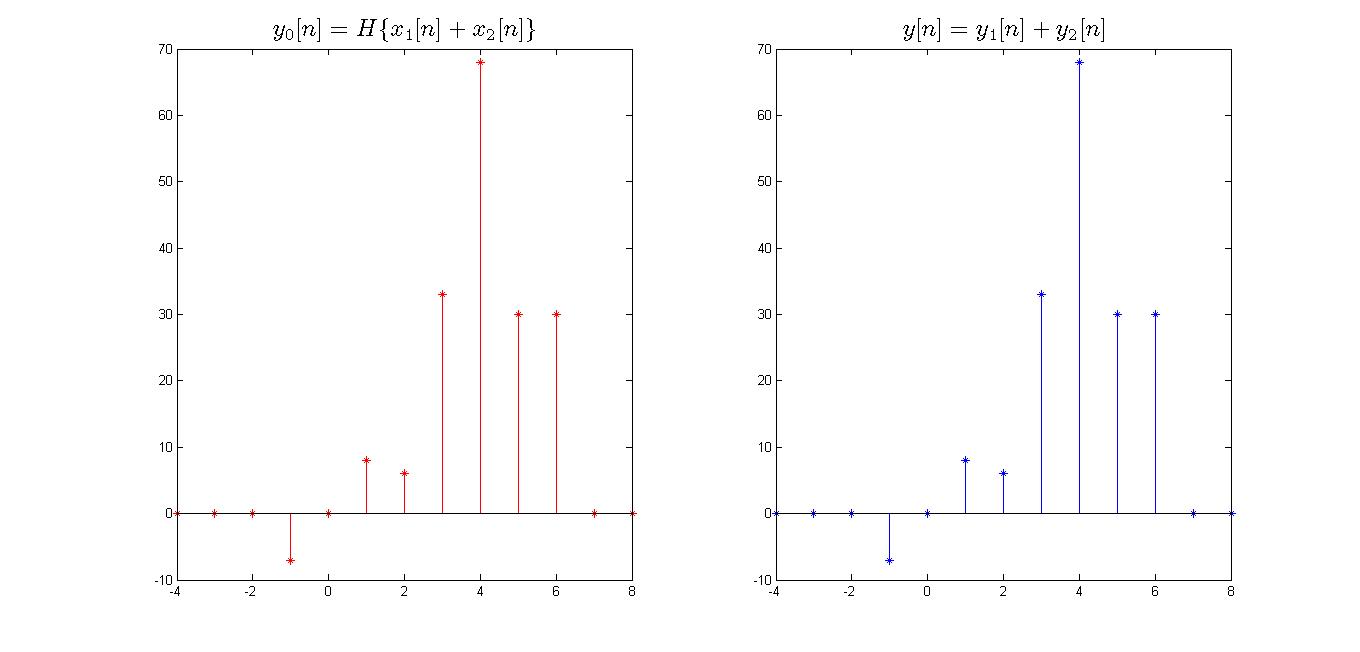
De esta forma, se obtiene a y0[n] como la seΓ±al de salida ante la entrada al sistema de la suma de x1[n] y x2[n]; por otra parte, se obtiene la suma de y1[n] con y2[n]; donde y1[n] y y2[n] son las seΓ±ales de salida para las entradas x1[n] y x2[n], respectivamente. Finalmente, al comparar las grΓ‘ficas de y0[n] y y1[n]β +β y2[n] se puede observar que el sistema es lineal ante las entradas x1[n] y x2[n].
CΓ³digo en matlab:
n=[-4,-3,-2,-1,0,1,2,3,4,5,6,7,8];
β
%--------------------------------------------%
%Definir las seΓ±al de entrada x1[n] y x2[n]
%n--> -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
x1=[0 0 4 6 3 1 5 9 2 4 0 0 0];
x2=[0 0 3 4 5 2 6 8 4 1 0 0 0];
β
%--------------------------------------------%
%Obtener tamaΓ±o de las seΓ±ales
N=length(x1);
β
%--------------------------------------------%
%Obtener y0[n]=H{x1[n]+x2[n]}
x1MASx2 = x1+x2;
for k=2:1:N
y0(k)=(n(k))*x1MASx2(k-1);
end
β
%--------------------------------------------%
%Obtener y1[n] y y2[n]
for k=2:1:N
y1(k) = (n(k))*x1(k-1);
y2(k) = (n(k))*x2(k-1);
end
β
%--------------------------------------------%
%Sumar y1[n] y y2[n]; y=y1[n]+y2[n]
y = y1+y2;
β
%--------------------------------------------%
%Graficar y0[n] y y[n]
β
%GrΓ‘fica de y0[n]
subplot(1,2,1)
stem(n,y0,β*-rβ)
β
%GrΓ‘fica de y[n]
subplot(1,2,2)
stem(n,y,β*-β)
Sistemas nivel avanzado:
- y[n]β =β x[n]β +β x[β ββ nβ ββ 1]
- y[n]β =β x[n]β ββ x[β ββ nβ +β 1]
- y[n]β =β u[n]x[n]
- y[n]β =β β§β¨β© x[n] x[n]β β₯β 0 β β β β ββ x[n] x[n]β <β 0 β«β¬β
- y[n]β =β βnkβ =β β ββ β(0.5)nβ ββ kx[k]
- y(t)β =β bβ«x(t) dt
- y[n]β =β x[nβ +β 1]β +β x[β ββ nβ +β 1]
- y[n]β =β x[nβ +β 1]x[β ββ nβ +β 1]
- y[n]β =β Par{x[n]}β +β x[nβ ββ 1]
- y[n]β =β Impar{x[n]}β ββ x[β ββ nβ +β 1]
Linealidad
y[n]β =β x[n]β +β x[β ββ nβ ββ 1] β
Se proponen tres entradas x1[n], x2[n] y x3[n]β =β x1[n]β +β x2[n], entonces las respectivas salidas son
y1[n]β =β x1[n]β +β x1[β ββ nβ ββ 1] β y2[n]β =β x2[n]β +β x2[β ββ nβ ββ 1] β y3[n]β =β x3[n]β +β x3[β ββ nβ ββ 1] β y3[n]β =β x1[n]β +β x2[n]β +β x1[β ββ nβ ββ 1]β +β x2[β ββ nβ ββ 1] β y tambiΓ©n β y3[n]β =β y1[n]β +β y2[n] β β΄Es lineal
Se propone una nueva seΓ±al x1[n] que es la original desplazada, con la que se obtiene la salida y1[n]
Se observa que salidas en tiempos presentes requieren de entradas en tiempos pasados y en tiempos futuros,
y[n]β =β x[n]β ββ x[β ββ nβ +β 1] β
Se proponen tres entradas x1[n], x2[n] y x3[n]β =β x1[n]β +β x2[n], entonces las respectivas salidas son
y1[n]β =β x1[n]β ββ x1[β ββ nβ +β 1] β y2[n]β =β x2[n]β ββ x2[β ββ nβ +β 1] β y3[n]β =β x3[n]β ββ x3[β ββ nβ +β 1] β y3[n]β =β x1[n]β +β x2[n]β ββ x1[β ββ nβ +β 1]β ββ x2[β ββ nβ +β 1] β y tambiΓ©n β y3[n]β =β y1[n]β +β y2[n] β β΄El sistema es lineal
y[n]β =β u[n]x[n] β y[β ββ 1]β =β u[β ββ 1]x[β ββ 1]β =β 0 β y[0]β =β u[0]x[0]β =β x[0] β y[1]β =β u[1]x[1]β =β x[1] β y[2]β =β u[2]x[2]β =β x[2] β ... β
Ya que la salida no depende de la entrada en instantes futuros el sistema es causal o no anticipativo.
El Sistema es estΓ‘tico o sin memoria debido a que depende la salida depende de la entrada en el mismo instante.
Se propone una entrada acotada en amplitud, como por ejemplo un escalΓ³n unitario. El sistema es estable BIBO ya que una multiplicaciΓ³n de escalones siempre serΓ‘ acotada en amplitud.
Si la seΓ±al de entrada se desplaza un tiempo n0, ese deslazamiento se verΓ‘ reflejado en la salida.
El sistema es Causal o no anticipativo, debido a que la salida sΓ³lo depende de la entrada en los mismos instantes, es decir, no depende de instantes posteriores.
El sistema es sin memoria, pues sΓ³lo depende de valores presentes de la entrada.
El sistema es estable BIBO ya que a una entrada acotada propuesta genera una salida acotada.
La estabilidad BIBO implica entradas acotadas, salidas acotadas, de manera que si se aplica al sistema una entrada escalΓ³n se obtendrΓ‘ a la salida una rampa, la integral del escalΓ³n. Por lo tanto el sistema no es estable desde el punto de vista BIBO.
y[n]β =β x[nβ +β 1]β +β x[β ββ nβ +β 1]
Analizando la estabilidad BIBO del sistema, se tiene que es estable BIBO debido a que la suma de dos seΓ±ales acotadas genera una seΓ±al tambien acotada.
Analizando la linealidad del sistema, se tiene que:
x[nβ +β 1]β =β x[nβ ββ n0β +β 1] β x[β ββ nβ +β 1]β =β x[β ββ nβ +β 1β ββ n0] β
Evaluando en distintos instantes de tiepo, se tiene:
Considerando una seΓ±al de entrada acotada en amplitud, se observa que la suma de tres seΓ±ales acotadas siempre generarΓ‘ una seΓ±al acotada, por lo tanto el sistema es estable BIBO.
Considerando una seΓ±al de entrada acotada en amplitud, se observa que la suma de tres seΓ±ales acotadas siempre generarΓ‘ una seΓ±al acotada, por lo tanto el sistema es estable BIBO.
Sistemas Lineales Invariantes en el Tiempo en TC:
En los ejemplos con soluciΓ³n de esta secciΓ³n se abordan conceptos, caracterΓsticas y formas de anΓ‘lisis fundamentales de los sistemas lineales e invariantes en el tiempo continuo. Se lleva a cabo el anΓ‘lisis de sistemas al obtener la respuesta de sistemas lineales e invariantes, mediante la integral de convoluciΓ³n y la transformada de la Laplace.
Selecciona la dificultad en las caritas de la izquierda.
Sistemas Lineales Invariantes en el Tiempo en TC nivel principiante:
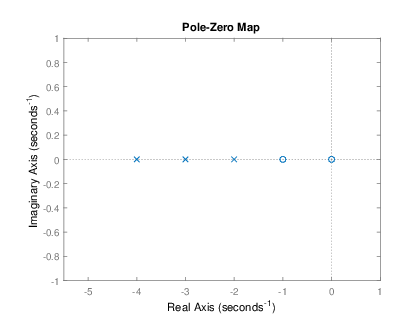
Suponga que se tiene la siguiente funciΓ³n de transferencia de un sistema, grafique el patrΓ³n de polos y ceros:
, cuyas raΓces o ceros son: y
, cuyas raΓces o polos son: , y
El patrΓ³n de polos y ceros es el siguiente:
Sistemas Lineales Invariantes en el Tiempo en TC nivel intermedio:
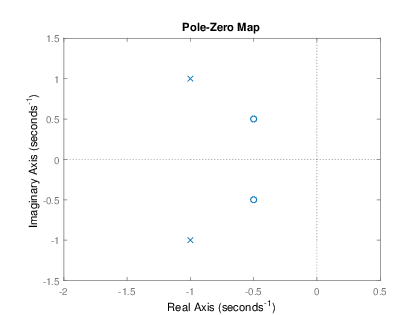
Considere la siguiente funciΓ³n de transferencia de un sistema, grafique el patrΓ³n de polos y ceros:
Se calculan las raΓces de los polinomios P(s) y Q(s) de la funciΓ³n de transferencia:
, cuyas raΓces o ceros son complejas conjugadas: y
, cuyas raΓces o polos son complejas conjugadas: y
El patrΓ³n de polos y ceros es el siguiente:
Sistemas Lineales Invariantes en el Tiempo en TC nivel avanzado:
- La funciΓ³n de transferencia, H(s).
- La respuesta el impulso, h(t), el valor de ΞΎ y el comportamiento del sistema.
- El diagrama de polos y ceros.
- La respuesta y(t) si la entrada es un escalΓ³n, x(t)β =β u(t).
- La respuesta y(t) si la entrada es un escalΓ³n, x(t)β =β u(t), y el sistema tiene las condiciones iniciales de y(0)β =β 1 y yβ(0)β =β 0.
- La respuesta y(t) si la entrada es una seΓ±al exponencial, y el sistema no tiene las condiciones iniciales.
- La respuesta y(t) si la entrada es una seΓ±al exponencial, y el sistema no tiene condiciones iniciales.
Con kβ
=β
6
Ya que H(s) es una funciΓ³n propia, es decir, mβ <β n, las raΓces son reales y diferentes s1β =β β ββ 2 y s2β =β β ββ 5, por lo que se tiene el caso de polos simples con los cuales se puede expresar la funciΓ³n de transferencia mediante factores como
y
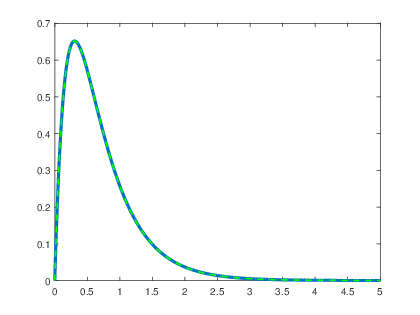
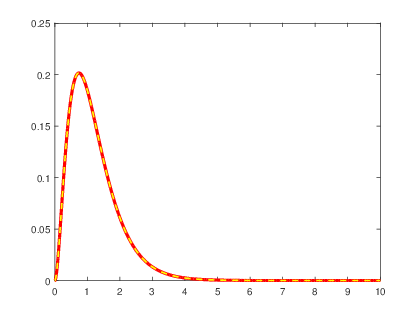
Se verifica la respuesta mediante simulaciΓ³n obteniendo la grΓ‘fica de la respuesta al impulso por medio de la funciΓ³n impulse() y se compara con la grΓ‘fica del resultado obtenido anteriormente.
>> a=[1 7 10];
>> b=6;
>> t=0:0.001:5;
>> h=impulse(b,a,t);
>> plot(t,h,βlinewidthβ,3);
>> hold on
>>x=(-2.*exp(-5.*t)+2.*exp(-2.*t)).*us(t);
>> plot(t,x,βg--β,βlinewidthβ,1.5);
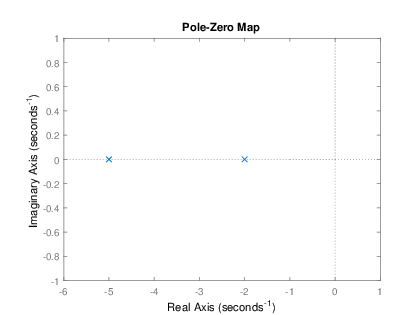
>> a=[1 7 10];
>> b=6;
>> pzmap(b,a);
4) El comportamiento y(t) si la entrada es un escalΓ³n, x(t)β =β u(t), es decir, la respuestadel de estado cero:
Encontrando, mediante expansiΓ³n en fracciones parciales, que los coeficientes A, B y C son :
Por lo que
En donde la respuesta permanentes es
y la respuesta tranasitoria es
Obteniendo la grΓ‘fica de la respuesta al escalΓ³n por medio de la funciΓ³n step() de Matlab y verificΓ‘ndola con la respuesta que se obtiene:
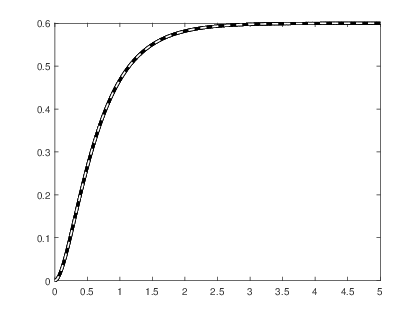
>> a=[1 7 10];
>> b=6;
>> t=0:0.001:5;
>> s=step(b,a,t);
>> plot(t,s,βkβ,βlinewidthβ,3);
>> hold on
>> x=(((2/5).*exp(-5.*t))-(exp(-2.*t))+(3/5)).*us(t);
>> plot(t,x,βw--β,βlinewidthβ,1.5);
o bien
En el inciso anterior se obtuvo la transformada inversa de Laplace del primer tΓ©rmino de Y(s), por lo que ahora sΓ³lo se obtiene la transformada inversa de Laplace para el segundo tΓ©rmino:
en donde la respuesta de estado cero es:
de manera que
Por lo tanto:
Aplicando la transformada inversa de Laplace a Y(s) se obtiene:
>> a=[1 7 10];
>>b=6;
>>t=0:0.001:10;
>>f=exp(-2.*t).*us(t);
>>y=lsim(b,a,f,t);
>>plot(t,y,βrβ,βlinewidthβ,3);
>>hold on
>>x=((2/3).*exp(-5.*t)-(2/3).*exp(-2.*t)+2.*t.*exp(-2.*t)).*us(t);
>>plot(t,x,βy--β,βlinewidthβ,1.5);
de manera que
Por lo tanto:
Aplicando la transformada inversa de Laplace a Y(s) se obtiene:
Se verifica que la respuesta obtenida corresponde con la simulada utilizando las funciones exp() y lsim():
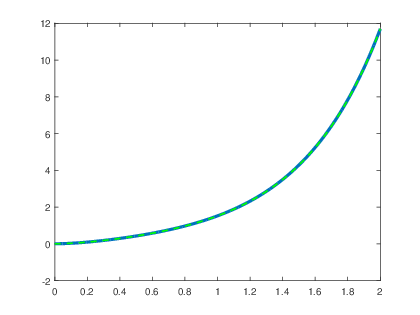
>> a=[1 7 10];
>> b=6;
>> t=0:0.001:2;
>> f=exp(2.*t).*us(t);
>> y=lsim(b,a,f,t);
>>plot(t,y,βlinewidthβ,3);
>>hold on
>>x=((2/7).*exp(-5.*t)-0.5.*exp(-2.*t)+(3/14).*exp(2.*t)).*us(t);
>>plot(t,x,βg--β,βlinewidthβ,1.5);
Con kβ =β 5
Ya que H(s) es una funciΓ³n propia, es decir, mβ <β n, las raΓces son reales e iguales, s1β =β s2β ββ 3, por lo que se tiene el caso de polos simples iguales con los cuales se puede expresar la funciΓ³n de transferencia mediante un factor duplicado como
A partir deH(s) se determina Οn y ΞΎ.
y
Se verifica la respuesta con Matlab obteniendo la grΓ‘fica de la respuesta al impulso por medio de la funciΓ³n impulse() y se compara con la grΓ‘fica del resultado obtenido anteriormente.
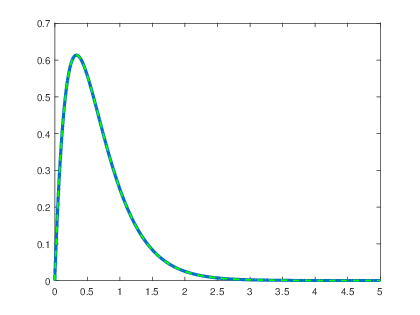
>> a=[1 6 9]; >> b=5; >> t=0:0.001:5; >> h=impulse(b,a,t); >> plot(t,h,βlinewidthβ,3); >> hold on >> x=5.*t.*exp(-3.*t).*us(t); >> plot(t,x,βg--β,βlinewidthβ,1.5);
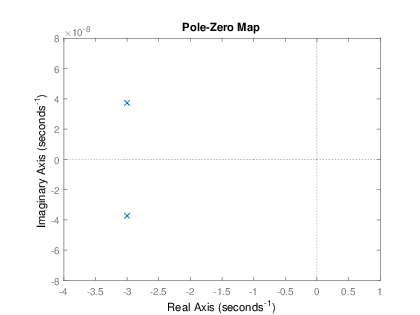
>> a=[1 6 9]; >> b=5; >> pzmap(b,a);
4) La respuesta y(t) si la entrada es un escalΓ³n, x(t)β =β u(t), la cual corresponde a una respuesta de estado cero.
Encontrando, mediante expansiΓ³n en fracciones parciales, que los coeficientes A, B y C son :
Por lo que
En donde la respuesta permanente es
y la respuesta transitoria es
La grΓ‘fica de la respuesta al escalΓ³n se obtiene por medio de la funciΓ³n step() de Matlab y se verifica con la respuesta que se obtuvo:
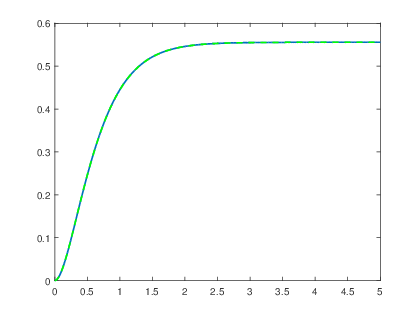
>> a=[1 6 9]; >> b=5; >> t=0:0.001:5; >> s=step(b,a,t); >> hold on >> x=(-(5/3).*t.*exp(-3.*t)-(5/9).*exp(-3.*t)+(5/9)).*us(t); >> plot(t,s,t,x,βw--β,βlinewidthβ,1.5);
o bien
La respuesta de entrada cero corresponde al segundo tΓ©rmino, a la que se encuentra su transformada inversa
en donde la respuesta de estado cero es:
de manera que
Por lo tanto:
Aplicando la transformada inversa de Laplace a Y(s) se obtiene:
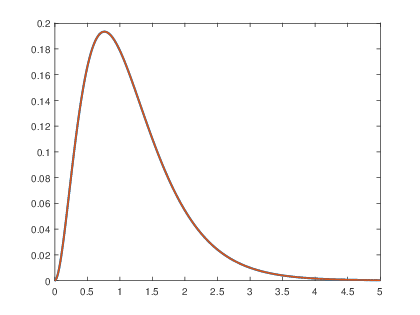
>> a=[1 6 9]; >> b=5; >> t=0:0.001:5; >> f=exp(-2.*t).*us(t); >> y=lsim(b,a,f,t); >> plot(t,y,βkβ,βlinewidthβ,3); >> hold on >> x=(5.*(-t.*exp(-3.*t)-exp(-3.*t)+exp(-2.*t))).*us(t); >> plot(t,x,βy--β,βlinewidthβ,1.5); β
de manera que
Por lo tanto:
Aplicando la transformada inversa de Laplace a Y(s) se obtiene:

>> a=[1 6 9]; >> b=5; >> t=0:0.001:5; >> f=exp(2.*t).*us(t); >> y=lsim(b,a,f,t); >> plot(t,y,βlinewidthβ,3); >> hold on >> x=(-t.*exp(-3.*t)-(1/5).*exp(-3.*t)+(1/5).*exp(2.*t)).*us(t); >> plot(t,x,βg--β,βlinewidthβ,1.5);
Con kβ =β 1
y
Se verifica la respuesta mediante simulaciΓ³n obteniendo la grΓ‘fica de la respuesta al impulso por medio de la funciΓ³n impulse() y se compara con la grΓ‘fica del resultado obtenido anteriormente.
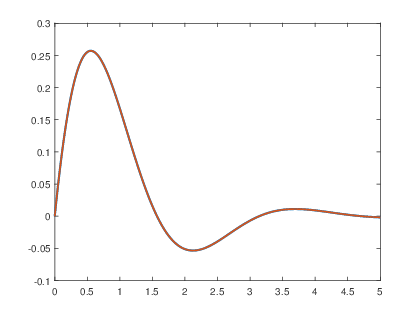
>> a=[1 2 5]; >> b=1; >> t=0:0.001:5; >> h=impulse(b,a,t); >>plot(t,h,βlinewidthβ,3) >>hold on >>x=0.5.*sin(2.*t).*exp(-t).*us(t); >>plot(t,x,βg--β,βlinewidthβ,1.5)
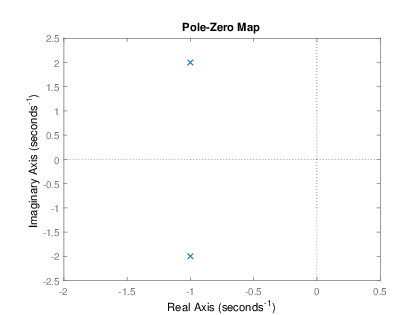
>> a=[1 2 5]; >> b=1; >> pzmap(b,a);
4) La respuesta y(t) si la entrada es un escalΓ³n, x(t)β =β u(t), la cual corresponde a la respuesta de estado cero yzs(t), ya que no se incluyen condiciones iniciales.
En donde la respuesta permanentes es
y la respuesta transitoria es
Obteniendo la grΓ‘fica de la respuesta al escalΓ³n por medio de la funciΓ³n step() de Matlab y verificΓ‘ndola con la respuesta que se obtiene:
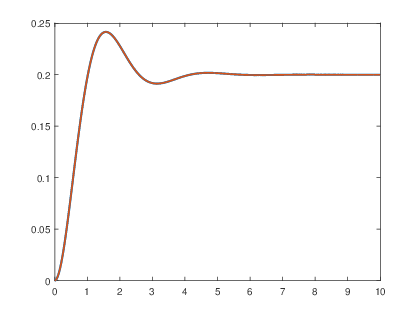
>> a=[1 2 5]; >> b=1; >> t=0:0.01:10; >> s=step(b,a,t); >> plot(t,s,βrβ,βlinewidthβ,3); >> hold on >> x=(-0.2.*exp(-t).*cos(2.*t)-0.1.*exp(-t).*sin(2.*t)+0.2).*us(t); >> plot(t,x,βy--β,βlinewidthβ,1.5);
o bien
En el inciso anterior se obtuvo la transformada inversa de Laplace del primer tΓ©rmino de Y(s), por lo que ahora sΓ³lo se obtiene la transformada inversa de Laplace para el segundo tΓ©rmino, la cual corresponde a la respuesta de entrada cero:
en donde la respuesta de estado cero ha sido determinada en el inciso anterior,
de manera que
Por lo tanto:
Aplicando la transformada inversa de Laplace a Y(s) se obtiene:
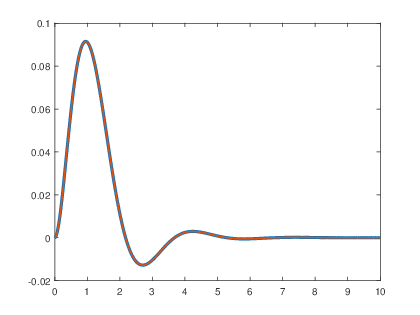
>> a=[1 2 5]; >>b=1; >>t=0:0.01:10; >>f=exp(-2.*t).*us(t); >>y=lsim(b,a,f,t); >>plot(t,y,βbβ,βlinewidthβ,3); >>hold on >>x=(-0.2.*exp(-t).*cos(2.*t)+0.1.*exp(-t).*sin(2.*t)+0.2.*exp(-2.*t)).*us(t); >>plot(t,x,βw--β,βlinewidthβ,1.5);
7) Si , la respuesta y(t) sin condiciones iniciales es:
de manera que
Por lo tanto:
Aplicando la transformada inversa de Laplace a Y(s) se obtiene:
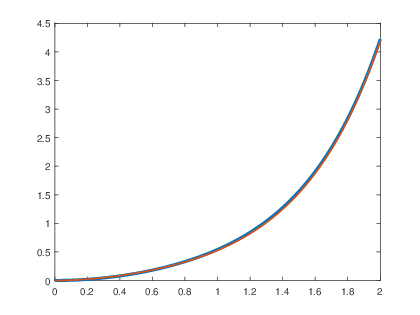
>> a=[1 2 5]; >>b=1; >>t=0:0.01:10; >>f=exp(2.*t).*us(t); >>y=lsim(b,a,f,t); >>plot(t,y,βkβ,βlinewidthβ,3); >> hold on >>x=(-(1/13).*exp(-2.*t).*cos(t)-(4/13).*exp(-2.*t).*sin(t)+... (1/13).*exp(2.*t)).*us(t); >> plot(t,x,βw--β,βlinewidthβ,1.5);
Con kβ =β β ββ 1
En este caso las raΓces son imaginarias conjugadas , por lo que se tiene el caso de polos en el eje imaginario.
Se verifica la respuesta mediante simulaciΓ³n obteniendo la grΓ‘fica de la respuesta al impulso por medio de la funciΓ³n impulse() y se compara con la grΓ‘fica del resultado obtenido anteriormente.
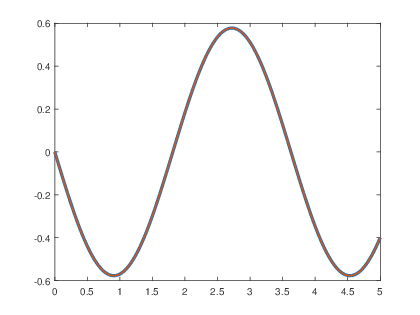
>>a=[1 0 3];
>>b=-1;
>>c=sqrt(3);
>>t=0:0.001:5;
>>h=impulse(b,a,t);
p>>lot(t,h, βlinewidthβ,3);
>>hold on
>>x=(-1/c).*sin(c.*t).*us(t);
>>plot(t,x,βg--β,βlinewidthβ,1.5)
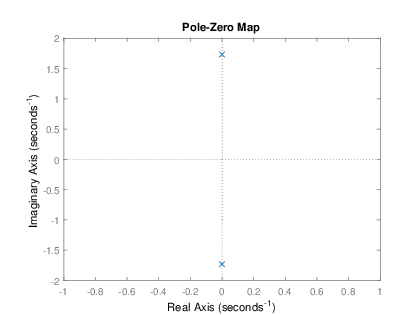
>> a=[1 0 3];
>> b=-1;
>> pzmap(b,a);
4) La respuesta y(t) si la entrada es un escalΓ³n, x(t)β =β u(t), la cual corresponde a una respuesta de estado cero.
Encontrando, mediante expansiΓ³n en fracciones parciales, que los coeficientes A, B y C son:
por lo que
En donde la respuesta permanentes tambiΓ©n es
y no hay respuesta transitoria.
La grΓ‘fica de la respuesta al escalΓ³n se obtiene por medio de la funciΓ³n step(), la cual se verifica con la respuesta que obtenida analΓticamente:
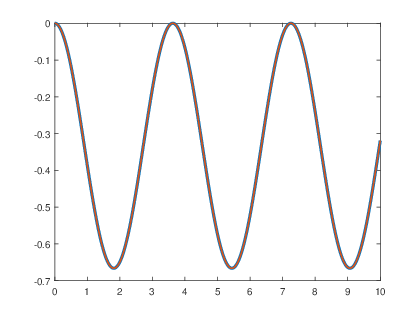
>> a=[1 0 3];
>> b=-1;
>>c=sqrt(3);
>> t=0:0.01:10;
>> s=step(b,a,t);
>> plot(t,s,βrβ,βlinewidthβ,3);
>> hold on
>> x=(-(1/3)+(1/3).*cos(c.*t)).*us(t);
>> plot(t,x,βy--β,βlinewidthβ,1.5);
o bien
En el inciso anterior se obtuvo la transformada inversa de Laplace del primer tΓ©rmino de Y(s), por lo que ahora sΓ³lo se obtiene la transformada inversa de Laplace para el segundo tΓ©rmino:
en donde la respuesta de estado cero es:
de manera que
Por lo tanto:
Al obtener la transformada inversa de Laplace de Y(s) se encuentra
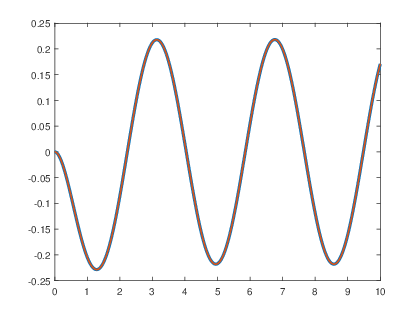
>>a=[1 0 3];
>>b=-1;
>>c=sqrt(3);
>>t=0:0.01:10;
>>f=exp(-2.*t).*us(t);
>>y=lsim(b,a,f,t);
>>plot(t,y,βbβ,βlinewidthβ,3);
>>hold on
>>x=(-(1/7).*exp(-2.*t)+(1/7).*cos(c.*t)-(2/(7.*c)).*sin(c.*t)).*us(t);
>>plot(t,x,βw--β,βlinewidthβ,1.5);
de manera que
Por lo tanto:
Aplicando la transformada inversa de Laplace a Y(s) se obtiene:
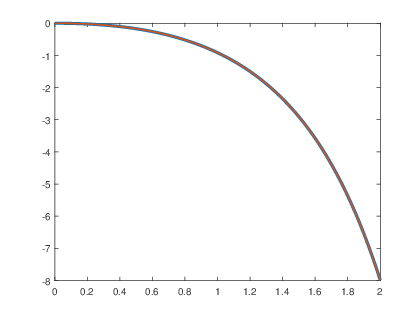
>>a=[1 0 3];
>>b=-1;
>>c=sqrt(3);
>>t=0:0.01:2;
>>f=exp(2.*t).*us(t);
>>y=lsim(b,a,f,t);
>>plot(t,y,βkβ,βlinewidthβ,3);
>>hold on
>>x=(-(1/7).*exp(-2.*t)+(1/7).*cos(c.*t)-(2/(7.*c)).*sin(c.*t)).*us(t);
>>plot(t,x,βw--β,βlinewidthβ,1.5);
Sistemas lineales e invariantes en el tiempo en TD:
En los ejemplos con soluciΓ³n de esta secciΓ³n se abordan conceptos, caracterΓsticas y formas de anΓ‘lisis fundamentales de los sistemas lineales e invariantes en el tiempo discreto. Se lleva a cabo el anΓ‘lisis de sistemas al obtener la respuesta de sistemas lineales e invariantes, mediante la suma de convoluciΓ³n y la transformada Z.
Selecciona la dificultad en las caritas de la izquierda.
Sistemas lineales e invariantes en el tiempo en TD nivel principiante:
- Obtenga H(z) y diga si es o no estable el sistema.
- Determine el diagrama de bloques del sistema.
- Obtenga los primeros 5 valores de h[n] mediante recursividad.
- Obtenga la respuesta al escalΓ³n mediante convoluciΓ³n.
SoluciΓ³n
-
Se tiene que h[n]β =β (1.5nβ +β 0.2nβ ββ 1)u[n]Aplicando leyes de los exponentes axβ +β yβ =β axayh[n]β =β (1.5nβ +β 0.2n0.2β ββ 1)u[n]h[n]β =β (1.5nβ +β 5(0.2)n)u[n]Se puede observar que h[n] tiene la forma de anu[n] y se sabe que la transformada de anu[n] esanu[n]β ββ (1)/(1β ββ azβ ββ 1)
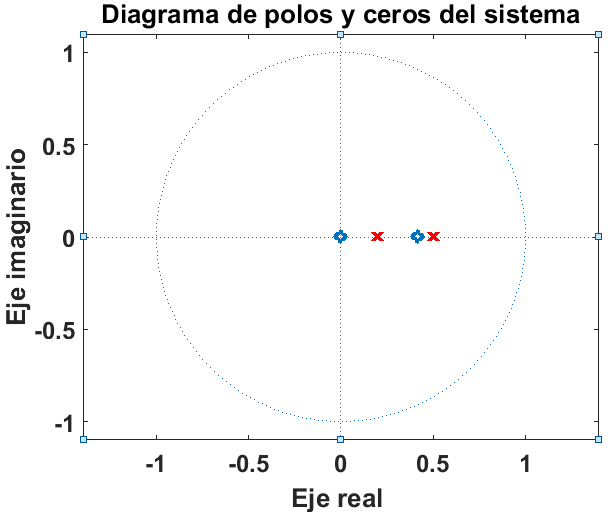
EntoncesH(z)β =β (1)/(1β ββ 1.5zβ ββ 1)β +β (5)/(1β ββ 0.2zβ ββ 1)DesarrollandoH(z)β =β (1β ββ 0.2zβ ββ 1β +β 5β ββ 1.5zβ ββ 1)/((1β ββ 7.5zβ ββ 1)(1β ββ 0.2zβ ββ 1))Por lo que H(z)β΄H(z)β =β (6β ββ 7.7zβ ββ 1)/((1β ββ 1.5zβ ββ 1)(1β ββ 0.2zβ ββ 1))β ββ H(z)β =β (6β ββ 7.7zβ ββ 1)/(1β ββ 1.7zβ ββ 1β +β 0.3zβ ββ 2)El sistema es inestable ya que una de sus raΓces es 1.5TambiΓ©n se puede observar por el diagrama de polos y ceros
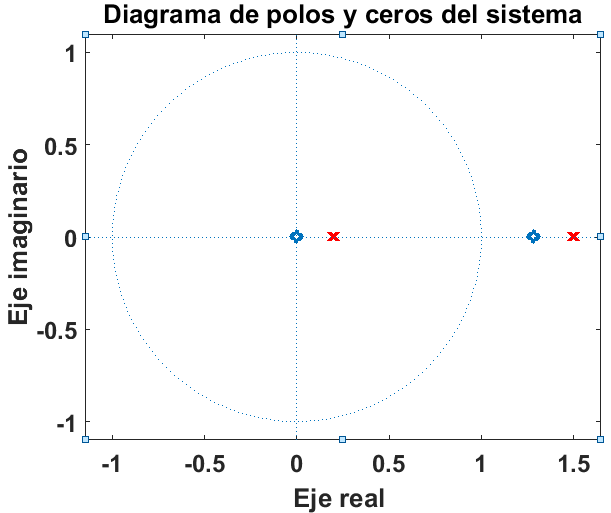 Figure 1.1βDiagrama de polos y ceros
Figure 1.1βDiagrama de polos y ceros
% Ejercicio 1 a=[1 -1.7 0.3]; b=[6 -7.7 0]; zplane(b,a); ylabel(βEje imaginarioβ); xlabel(βEje real β); title(βDiagrama de polos y ceros del sistemaβ);
-
De acuerdo a H(z)H(z)β =β (6β ββ 7.7zβ ββ 1)/(1β ββ 1.7zβ ββ 1β +β 0.3zβ ββ 2)Obteniendo la ecuaciΓ³n en diferencias:y[n]β ββ 1.7y[nβ ββ 1]β +β 0.3y[nβ ββ 2]β =β 6x[n]β ββ 7.7x[nβ ββ 1] β y[n]β =β 1.7y[nβ ββ 1]β ββ 0.3y[nβ ββ 2]β +β 6x[n]β ββ 7.7x[nβ ββ 1]El diagrama de bloques:
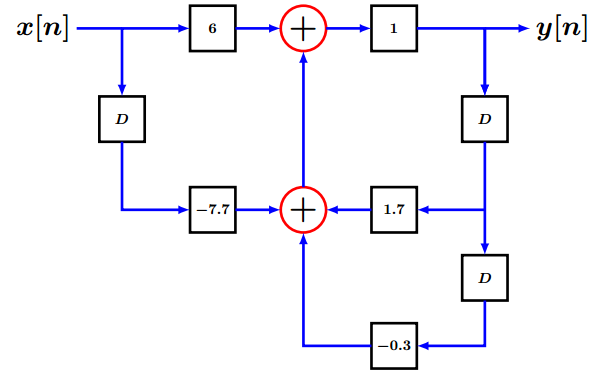 Figure 1.2βDiagrama de bloques.
Figure 1.2βDiagrama de bloques. -
Por el mΓ©todo de recursividady[n]β =β 1.7y[nβ ββ 1]β ββ 0.3y[nβ ββ 2]β +β 6x[n]β ββ 7.7x[nβ ββ 1] β h[n]β =β 1.7h[nβ ββ 1]β ββ 0.3h[nβ ββ 2]β +β 6Ξ΄[n]β ββ 7.7Ξ΄[nβ ββ 1] β h[0]β =β 6 Ξ΄[0]β =β 6 β h[1]β =β 1.7h[0]β ββ 7.7Ξ΄[0]β =β 2.5 β h[2]β =β 1.7h[1]β ββ 0.3h[0]β =β 2.45 β h[3]β =β 1.7h[2]β ββ 0.3h[1]β =β 3.415 β h[4]β =β 1.7h[3]β ββ 0.3h[2]β =β 5.0705 β h[5]β =β 1.7h[4]β ββ 0.3h[3]β =β 7.59535
-
Si x[n]β
=β
u[n] y h[n]β
=β
(1.5nβ
+β
0.2nβ
ββ
1)u[n]Entoncesy[n]β =β x[n]*y[n] β y[n]β =β u[n]*y[n]Por conmutatividady[n]β =β h[n]*u[n]Aplicando la definiciΓ³ny[n]β =β h[n]*u[n] β y[n]β =β ββkβ =β β ββ βh[k]u[nβ ββ k] β y[n]β =β ββkβ =β β ββ β(1.5kβ +β 0.2kβ +β 1)u[k]u[nβ ββ k] β y[n]β =β ββkβ =β β ββ β1.5ku[k]u[nβ ββ k]β +β ββkβ =β β ββ β0.2kβ ββ 1u[k]u[nβ ββ k]Definiendo los lΓmitesu[n]β =β 1 nβ β₯β 0; u[k]β =β 1 kβ β₯β 0; u[nβ ββ k]β =β 1 nβ ββ kβ β₯β 0; kβ β€β n β β β β β β β u[n]β =β 0 nβ <β 0 u[k]β =β 0 kβ <β 0 u[nβ ββ k]β =β 0 nβ ββ kβ <β 0; kβ >β nEntoncesy[n]β =β β²β³nkβ =β 01.5kβ +β β²β³nkβ =β 00.2kβ ββ 1y[n]β =β β²β³nkβ =β 01.5kβ +β 0.2β ββ 1β²β³nkβ =β 00.2kPor series singularβ²β³nkβ =β 0akβ =β (1β ββ anβ +β 1)/(1β ββ a)y[n]β =β (1β ββ 1.5nβ +β 1)/(1β ββ 1.5)β +β (0.2β ββ 1)(1β ββ 0.2nβ +β 1)/(1β ββ 0.2) u[n]y[n]β =β β ββ 2(1β ββ (1.5)nβ +β 1)β +β 5((1β ββ (0.2)nβ +β 1))/((4)/(5)) u[n]El resultado es: y[n]β =β β ββ 2(1β ββ (1.5)nβ +β 1)β +β (25)/(4)(1β ββ (0.2)nβ +β 1) u[n]
- Obtenga H(z) y diga si es o no estable el sistema.
- Determine el diagrama de bloques del sistema.
- Obtenga los primeros 5 valores de h[n] mediante recursividad.
- Obtenga la respuesta al escalΓ³n mediante convoluciΓ³n.
SoluciΓ³n
-
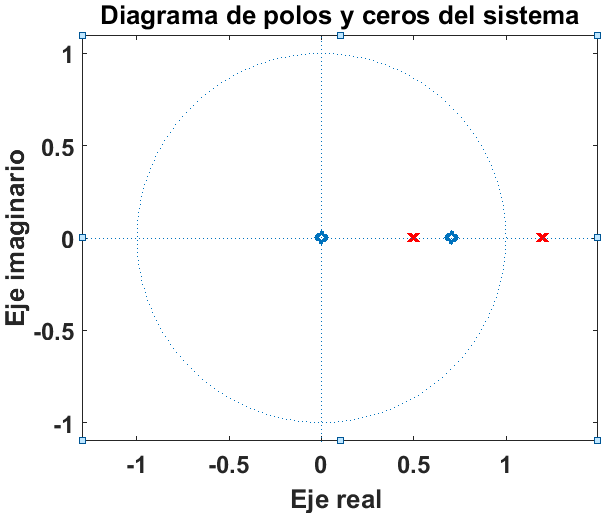
La respuesta h[n] tambiΓ©n puede expresarse comoh[n]β =β [(2)0.5nβ +β (5)0.2n)]u[n]Para determinar la estabilidad del sistema es necesario conocer el diagrama de polos y ceros, por lo tanto:Aplicando la transformada Z:2(0.5n)β =β (2)(1)/(1β ββ (1)/(2)zβ ββ 1) β 5(0.2n)β =β (5)(1)/(1β ββ (1)/(5)zβ ββ 1)Entonces:H(z)β =β (2)(1)/(1β ββ (1)/(2)zβ ββ 1)β +β (5)(1)/(1β ββ (1)/(5)zβ ββ 1)Sumando las fracciones:H(z)β =β (2ββ1β ββ (1)/(5)zβ ββ 1ββ β +β 5ββ1β ββ (1)/(2)zβ ββ 1ββ )/(ββ1β ββ (1)/(2)zβ ββ 1ββ ββ1β ββ (1)/(5)zβ ββ 1ββ ) β H(z)β =β (2β ββ (2)/(5)zβ ββ 1β +β 5β ββ (5)/(2)zβ ββ 1)/(1β ββ (1)/(2)zβ ββ 1β ββ (1)/(5)zβ ββ 1β +β (1)/(10)zβ ββ 2) β H(z)β =β (7β ββ (29)/(10)zβ ββ 1)/(1β ββ (7)/(10)zβ ββ 1β +β (1)/(10)zβ ββ 2)
Se llega a: y[n]β ββ (7)/(10)y[nβ ββ 1]β +β (1)/(10)y[nβ ββ 2]β =β 7x[n]β ββ (29)/(10)x[nβ ββ 1]Se analiza la estabilidad del sistema en donde los polos deben estar contenidos en el cΓrculo unitario:% Ejercicio 2 a=[1 -7/10 1/10]; b=[7 -29/10 0]; zplane(b,a); ylabel(βEje imaginarioβ); xlabel(βEje real β); title(βDiagrama de polos y ceros del sistemaβ);
-
De acuerdo con H(z)β
=β
(7β
ββ
(29)/(10)zβ
ββ
1)/(1β
ββ
(7)/(10)zβ
ββ
1β
+β
(1)/(10)zβ
ββ
2)
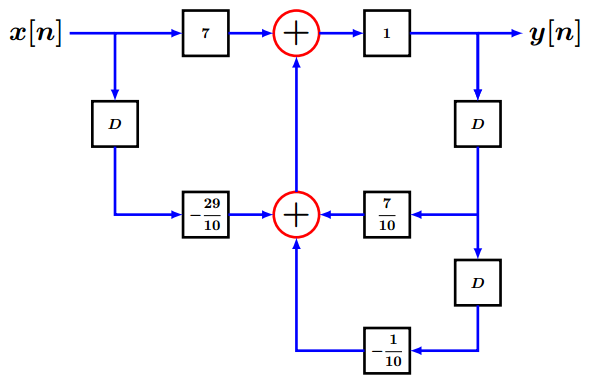 Figure 1.4βDiagrama de bloques.
Figure 1.4βDiagrama de bloques. -
Por el mΓ©todo de recursividad.y[n]β =β 7x[n]β ββ (29)/(10)x[nβ ββ 1]β +β (7)/(10)y[nβ ββ 1]β ββ (1)/(10)y[nβ ββ 2]Como no hay condiciones iniciales y la entrada es Ξ΄[n], se tiene que:h[0]β =β 7Ξ΄[0]β ββ (29)/(10)Ξ΄[β ββ 1]β +β (7)/(10)h[β ββ 1]β ββ (1)/(10)h[β ββ 2]β =β 7 β h[1]β =β 7Ξ΄[1]β ββ (29)/(10)Ξ΄[0]β +β (7)/(10)h[0]β ββ (1)/(10)h[β ββ 1]β =β 2 β h[2]β =β 7Ξ΄[2]β ββ (29)/(10)Ξ΄[1]β +β (7)/(10)h[1]β ββ (1)/(10)h[0]β =β 0.7 β h[3]β =β 7Ξ΄[3]β ββ (29)/(10)Ξ΄[2]β +β (7)/(10)h[2]β ββ (1)/(10)h[1]β =β 0.29 β h[4]β =β 7Ξ΄[4]β ββ (29)/(10)Ξ΄[3]β +β (7)/(10)h[3]β ββ (1)/(10)h[2]β =β 0.133 β h[5]β =β 7Ξ΄[5]β ββ (29)/(10)Ξ΄[4]β +β (7)/(10)h[4]β ββ (1)/(10)h[3]β =β 0.0641
-
Si x[n]β
=β
u[n] y h[n]β
=β
(0.5nβ
ββ
1β
+β
0.2nβ
ββ
1)u[n]y[n]β =β ββkβ =β β ββ β(h[k])(x[nβ ββ k]) β y[n]β =β βββ ββ ββ‘β£2ββ(1)/(2)ββ nβ +β 5ββ(1)/(5)ββ nu[n]β€β¦u[nβ ββ k] β y[n]β =β ββkβ =β β ββ β2ββ(1)/(2)ββ nu[n]u[nβ ββ k]β +β 5ββ(1)/(5)ββ nu[n]u[nβ ββ k] β y[n]β =β 2ββkβ =β β ββ βββ(1)/(2)ββ nu[n]u[nβ ββ k]β +β 5ββkβ =β β ββ βββ(1)/(5)ββ nu[n]u[nβ ββ k] β y[n]β =β 2βnkβ =β 0ββ(1)/(2)ββ nβ +β 5βnkβ =β 0ββ(1)/(5)ββ n β y[n]β =β β‘β’β’β£2(1β ββ (1)/(2)nβ +β 1)/(1β ββ (1)/(2))β +β 5(1β ββ (1)/(5)nβ +β 1)/(1β ββ (1)/(5))β€β₯β₯β¦u[n]
Sistemas lineales e invariantes en el tiempo en TD nivel intermedio:
- Obtenga H(z) y diga si es o no estable el sistema.
- Determine el diagrama de bloques del sistema.
- Obtenga los primeros 5 valores de h[n] mediante recursividad.
- Obtenga la respuesta al escalΓ³n mediante convoluciΓ³n.
SoluciΓ³n
-
De la funciΓ³n discreta h[n]β
=β
(0.5nβ
+β
1β
+β
0.2nβ
ββ
1)u[n] se tiene que:h[n]β =β (1)/(2)ββ(1)/(2)ββ nβ +β 5ββ(1)/(5)ββ n β H(z)β =β (1)/(2)βββ(z)/(zβ ββ (1)/(2))βββ β +β 5βββ(z)/(zβ ββ (1)/(5))βββObteniendo las raΓces: z1β =β (1)/(2)Β ;Β z2β =β (1)/(5)Como se observa, el sistema es estable ya que las raΓces del sistema caen dentro del cΓrculo unitario (su magnitud es menor a 1).
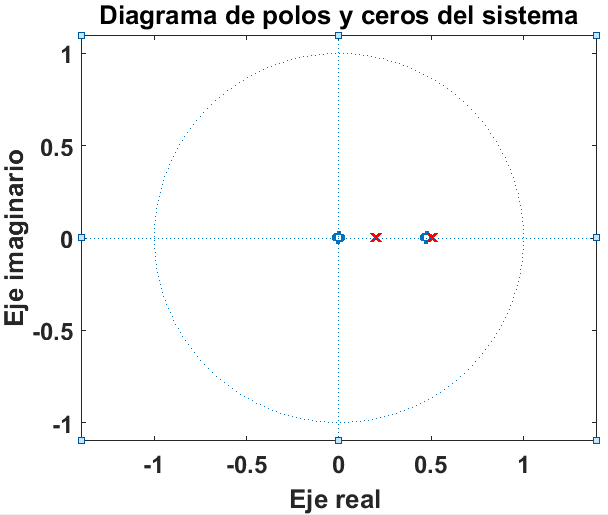 Figure 1.5βDiagrama de polos y ceros
Figure 1.5βDiagrama de polos y ceros
% Ejercicio 3 a=[1 -0.7 0.1]; b=[5.5 -2.6 0]; zplane(b,a); ylabel(βEje imaginarioβ); xlabel(βEje real β); title(βDiagrama de polos y ceros del sistemaβ);
-
Se reescribe la funciΓ³n de transferencia y se tiene que:H(z)β =β 0.5ββ(1)/(1β ββ 0.5zβ ββ 1)ββ β +β 5ββ(1)/(1β ββ 0.2zβ ββ 1)ββDesarrollando la expresiΓ³n:H(z)β =β (5.5β ββ 2.6zβ ββ 1)/(1β ββ 0.7zβ ββ 1β +β 0.1zβ ββ 2)Por lo que la ecuaciΓ³n en diferencias queda como:0.1y[nβ ββ 2]β ββ 0.7y[nβ ββ 1]β +β y[n]β =β 5.5x[n]β ββ 2.6x[nβ ββ 1]Despejando y[n]:y[n]β =β β ββ 0.1y[nβ ββ 2]β +β 0.7y[nβ ββ 1]β ββ 2.6x[nβ ββ 1]β +β 5.5x[n]El diagrama de bloques de dicho sistema es:
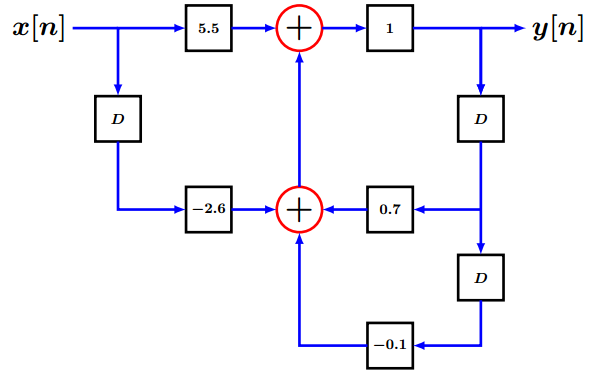 Figure 1.6βDiagrama de bloques.
Figure 1.6βDiagrama de bloques.
-
De la expresiΓ³n anterior se obtuvo que:y[n]β =β β ββ 0.1y[nβ ββ 2]β +β 0.7y[nβ ββ 1]β ββ 2.6x[nβ ββ 1]β +β 5.5x[n]Si x[n]β =β Ξ΄[n]:h[n]β =β β ββ 0.1h[nβ ββ 2]β +β 0.7h[nβ ββ 1]β ββ 2.6Ξ΄[nβ ββ 1]β +β 5.5Ξ΄[n]Por recursividad se obtiene que:h[0]β =β β ββ 0.1h[β ββ 2]β +β 0.7h[β ββ 1]β ββ 2.6Ξ΄[β ββ 1]β +β 5.5Ξ΄[0]β =β \bf5.5 β h[1]β =β β ββ 0.1h[β ββ 1]β +β 0.7h[0]β ββ 2.6Ξ΄[0]β +β 5.5Ξ΄[1]β =β (0.7*5.5)β ββ 2.5β =β \bf1.25 β h[2]β =β β ββ 0.1h[0]β +β 0.7h[1]β ββ 2.6Ξ΄[1]β +β 5.5Ξ΄[2]β =β (β ββ 0.1*5.5)β +β (0.7*1.25)β =β \bf0.325 β h[3]β =β β ββ 0.1h[1]β +β 0.7h[2]β ββ 2.6Ξ΄[2]β +β 5.5Ξ΄[3]β =β (β ββ 0.1*1.25)β +β (0.7*0.325)β =β \bf0.1025 β h[4]β =β β ββ 0.1h[2]β +β 0.7h[3]β ββ 2.6Ξ΄[3]β +β 5.5Ξ΄[4]β =β (β ββ 0.1*0.325)β +β (0.7*0.1025)β =β \bf0.03925 β
-
Se parte de h[n]β
=β
(0.5nβ
+β
1β
+β
0.2nβ
ββ
1)u[n]:x[n]β =β u[n] β y[n]β =β h[n]*x[n] β y[n]β =β ββkβ =β β ββ βh[k]x[nβ ββ k] β y[n]β =β ββkβ =β β ββ β(0.5kβ +β 1β +β 0.2kβ ββ 1)u[k]u[nβ ββ k] β y[n]β =β ββkβ =β β ββ β(0.5kβ +β 1u[k]u[nβ ββ k]β +β 0.2kβ ββ 1u[k]u[nβ ββ k]) β y[n]β =β (1)/(2)ββkβ =β β ββ β0.5ku[k]u[nβ ββ k]β +β 5ββkβ =β β ββ β0.2ku[k]u[nβ ββ k] β y[n]β =β (1)/(2)βnkβ =β 00.5kβ +β 5βnkβ =β 00.2k β y[n]β =β ββ(1)/(2)ββ(1β ββ 0.5nβ +β 1)/(1β ββ 0.5)ββ β +β 5ββ(1β ββ 0.2nβ +β 1)/(1β ββ 0.2)ββ ββ u[n] β y[n]β =β ββ0.5ββ(1β ββ 0.5nβ +β 1)/(0.5)ββ β +β 5ββ(1β ββ 0.2nβ +β 1)/(0.8)ββ ββ u[n] β y[n]β =β ββ1β +β (5)/(0.8)β ββ 0.5nβ +β 1β ββ (0.2n)/(0.8)ββ u[n] β y[n]β =β (7.25β ββ 0.5nβ +β 1β ββ 1.25(0.2n))u[n]
- Obtenga H(z) y diga si es o no estable el sistema.
- Determine el diagrama de bloques del sistema.
- Obtenga los primeros 5 valores de h[n] mediante recursividad.
- Obtenga la respuesta al escalΓ³n mediante convoluciΓ³n.
SoluciΓ³n
-
Se parte de la funciΓ³n discreta h[n]β
=β
(0.5nβ
+β
1β
+β
1.2nβ
+β
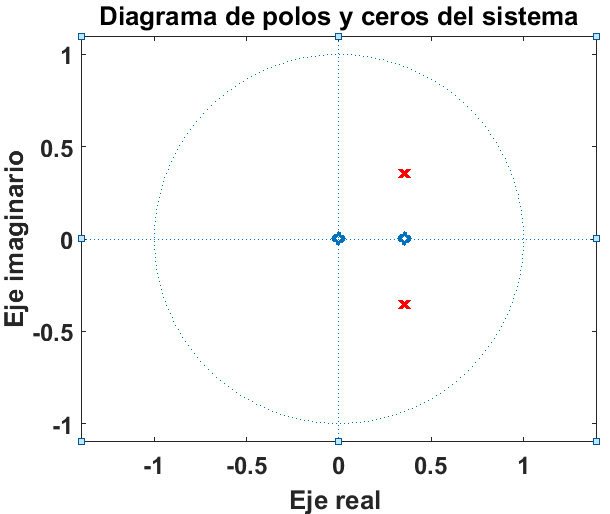
1)u[n]h[n]β =β 0.5nβ +β 1u[n]β +β 1.2nβ +β 1u[n] β h[n]β =β (0.5)0.5nu[n]β +β (1.2)1.2nu[n] β H(z)β =β (0.5)/(1β ββ 0.5zβ ββ 1)β +β (1.2)/(1β ββ 1.2zβ ββ 1) β H(z)β =β (0.5(1β ββ 1.2zβ ββ 1)β +β 1.2(1β ββ 0.5zβ ββ 1))/((1β ββ 0.5zβ ββ 1)(1β ββ 1.2zβ ββ 1)) β H(z)β =β (0.5β ββ 0.6zβ ββ 1β +β 1.2β ββ 0.6zβ ββ 1)/((1β ββ 0.5zβ ββ 1)(1β ββ 1.2zβ ββ 1)) β H(z)β =β (1.7β ββ 1.2zβ ββ 1)/((1β ββ 1.2zβ ββ 1)(1β ββ 0.5zβ ββ 1)) β H(z)β =β (1.7β ββ 1.2zβ ββ 1)/(1β ββ 1.2zβ ββ 1β ββ 0.5zβ ββ 1β +β 0.6zβ ββ 2) β H(z)β =β (1.7β ββ 1.2zβ ββ 1)/(1β ββ 1.7zβ ββ 1β +β 0.6zβ ββ 2)
% Ejercicio 4 a=[1 -1.7 0.6]; b=[1.7 -1.2 0]; zplane(b,a); ylabel(βEje imaginarioβ); xlabel(βEje real β); title(βDiagrama de polos y ceros del sistemaβ);
Como se observa en la imagen anterior el sistema es inestable, ya que un polo cae fuera del circulo unitario. -
De acuerdo con la funciΓ³n de transferencia H(z)β
=β
(1.7β
ββ
1.2zβ
ββ
1)/(1β
ββ
1.7zβ
ββ
1β
+β
0.6zβ
ββ
2)
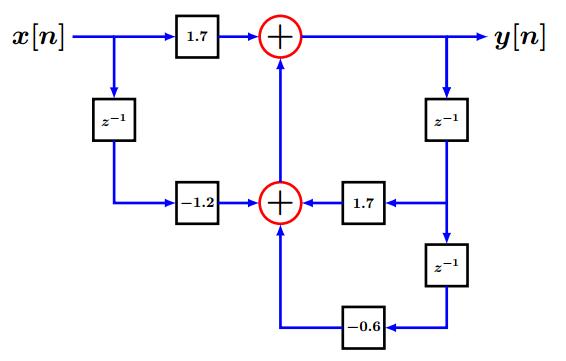 Figure 1.8βDiagrama de bloques.
Figure 1.8βDiagrama de bloques.
-
Mediante recursividad.H(z)β =β (1.7β ββ 1.2zβ ββ 1)/(1β ββ 1.7zβ ββ 1β +β 0.6zβ ββ 2)β =β (Y(z))/(X(z)) β h(z)(1β ββ 1.7zβ ββ 1β +β 0.6zβ ββ 2)β =β x(z)(1.7β ββ 1.2zβ ββ 1) β h(z)β ββ 1.7h(z)zβ ββ 1β +β 0.6h(z)zβ ββ 2β =β 1.7x(z)β ββ 1.2x(z)zβ ββ 1 β h[n]β ββ 1.7h[nβ ββ 1]β +β 0.6h[nβ ββ 2]β =β 1.7x[n]β ββ 1.2x[nβ ββ 1] β ConΒ x[n]β =β Ξ΄[n] β h[n]β =β 1.7h[nβ ββ 1]β ββ 0.6h[nβ ββ 2]β +β 1.7Ξ΄[n]β ββ 1.2Ξ΄[nβ ββ 1] β h[0]β =β 1.7h[β ββ 1]β ββ 0.6h[β ββ 2]β +β 1.7Ξ΄[0]β ββ 1.2Ξ΄[β ββ 1]β =β 1.7 β h[1]β =β 1.7h[0]β ββ 0.6h[β ββ 1]β +β 1.7Ξ΄[1]β ββ 1.2Ξ΄[0]β =β (1.7)(1.7)β +β 0β ββ 1.2β =β 1.69 β h[2]β =β 1.7h[1]β ββ 0.6h[0]β +β 1.7Ξ΄[2]β ββ 1.2Ξ΄[1]β =β (1.7)(1.69)β ββ (0.6)(1.7)β =β 1.853 β h[3]β =β 1.7h[2]β ββ 0.6h[1]β +β 1.7Ξ΄[3]β ββ 1.2Ξ΄[2]β =β (1.7)(1.853)β ββ (0.6)(1.69)β =β 2.1361 β h[4]β =β 1.7h[3]β ββ 0.6h[2]β +β 1.7Ξ΄[4]β ββ 1.2Ξ΄[3]β =β (1.7)(2.1361)β ββ (0.6)(1.8563)β =β 2.5195
-
Si h[n]β
=β
(0.5nβ
+β
1β
+β
1.2nβ
+β
1)u[n] con x[n]β
=β
u[n]y[n]β =β x[n]*h[n]β =β ββkβ =β β ββ βx[k]h[nβ ββ k] β y[n]β =β h[n]*x[n]β =β ββkβ =β β ββ βh[k]x[nβ ββ k] β y[n]β =β h[n]*x[n]β =β ββkβ =β β ββ β0.5kβ +β 1β +β 1.2kβ +β 1)u[k]u[nβ ββ k] β y[n]β =β ββkβ =β β ββ β0.5kβ +β 1u[k]u[nβ ββ k]β +β ββkβ =β β ββ β1.2kβ +β 1u[k]u[nβ ββ k] β y[n]β =β βnkβ =β 00.5kβ +β 1β +β βnkβ =β 01.2kβ +β 1β =β βnkβ =β 00.5k(0.5)β +β βnkβ =β 01.2k(1.2)β =β 0.5βnkβ =β 00.5kβ +β 1.2βnkβ =β 01.2k β ConΒ βNnβ =β 0Ξ±nβ =β (1β ββ Ξ±Nβ +β 1)/(1β ββ Ξ±) β y[n]β =β 0.5ββ(1β ββ 0.5nβ +β 1)/(1β ββ 0.5)ββ u[n]β +β 1.2ββ(1β ββ 1.2nβ +β 1)/(1β ββ 1.2)ββ u[n] β y[n]β =β (1β ββ 0.5nβ +β 1)u[n]β ββ 6(1β ββ 1.2nβ +β 1)u[n] β y[n]β =β (1β ββ 0.5nβ +β 1β ββ 6β +β (6)(1.2nβ +β 1))u[n] β y[n]β =β (β ββ 0.5nβ +β 1β +β (6)(1.2nβ +β 1)β ββ 5)u[n]
Sistemas lineales e invariantes en el tiempo en TD nivel avanzado:
- Obtenga H(z) y diga si es o no estable el sistema.
- Determine el diagrama de bloques del sistema.
- Obtenga los primeros 5 valores de h[n] mediante recursividad.
- Obtenga la respuesta al escalΓ³n mediante convoluciΓ³n.
SoluciΓ³n
-
Partiendo de la funciΓ³n discreta h[n]β
=β
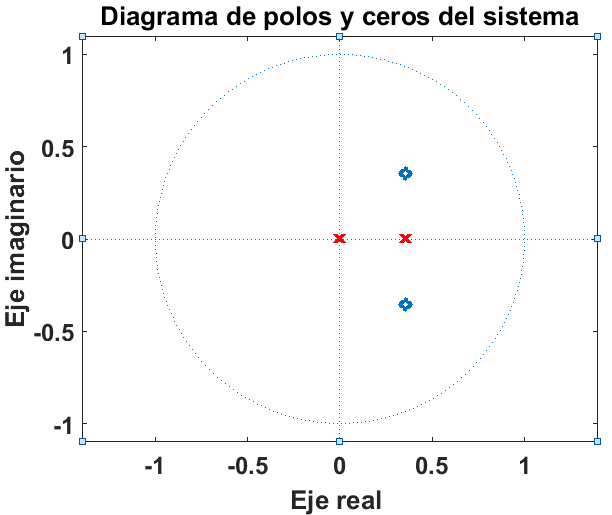
ββ0.5ncosββ(Οn)/(4)ββ ββ u[n]H(z)β =β (z2β ββ 0.5zcosββ(Ο)/(4)ββ )/(z2β ββ 2(0.5)zcosββ(Ο)/(4)ββ β +β 0.52) β H(z)β =β (z2β ββ (β(2))/(4)z)/(z2β ββ (β(2))/(2)zβ +β 0.25) β De donde: β z1β =β (β(2))/(4)β +β (β(2))/(4)j β z2β =β (β(2))/(4)β ββ (β(2))/(4)jLas raΓces son menores a uno, lo que nos indica que se encuentran dentro del cΓrculo unitario por lo que el sistema es estable.
% Ejercicio 5 a=[1 -sqrt(2)/2 0.25]; b=[1 -sqrt(2)/4 0]; zplane(b,a); ylabel(βEje imaginarioβ); xlabel(βEje real β); title(βDiagrama de polos y ceros del sistemaβ);
-
Diagrama de bloques H(z)β
=β
(z2β
ββ
(β(2))/(4)z)/(z2β
ββ
(β(2))/(2)zβ
+β
0.25)βΉH(z)β
=β
(1β
ββ
(β(2))/(4)zβ
ββ
1)/(1β
ββ
(β(2))/(2)zβ
ββ
1β
+β
0.25zβ
ββ
2)
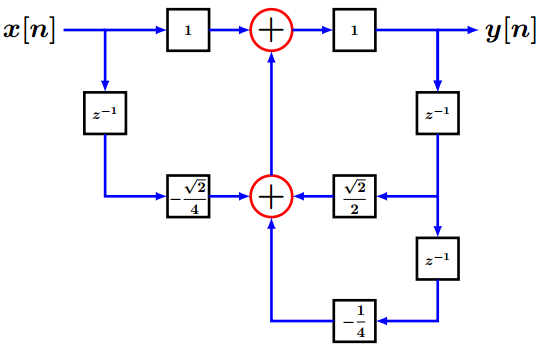 Figure 1.10βDiagrama de bloques.
Figure 1.10βDiagrama de bloques. -
Mediante recursividady[n]β ββ (β(2))/(2)y[nβ ββ 1]β +β (1)/(4)y[nβ ββ 2]β =β x[n]β ββ (β(2))/(4)x[nβ ββ 1] β y[n]β =β (β(2))/(2)y[nβ ββ 1]β ββ (1)/(4)y[nβ ββ 2]β +β x[n]β ββ (β(2))/(4)x[nβ ββ 1] β SiΒ x[n]β =β Ξ΄[n]Β entoncesΒ y[n]β =β h[n] β Evaluando en diferentes instantes β h[0]β =β (β(2))/(2)h[0β ββ 1]β ββ (1)/(4)h[0β ββ 2]β +β Ξ΄[0]β ββ (β(2))/(4)Ξ΄[0β ββ 1]β =β 1 β h[1]β =β (β(2))/(2)h[0]β ββ (1)/(4)h[β ββ 1]β +β Ξ΄[1]β ββ (β(2))/(4)Ξ΄[0]β =β 0.3536 β h[2]β =β (β(2))/(2)h[1]β ββ (1)/(4)h[0]β +β Ξ΄[2]β ββ (β(2))/(4)Ξ΄[1]β =β 0 β h[3]β =β (β(2))/(2)h[2]β ββ (1)/(4)h[1]β +β Ξ΄[3]β ββ (β(2))/(4)Ξ΄[2]β =β β ββ 0.0884 β h[4]β =β (β(2))/(2)h[3]β ββ (1)/(4)h[2]β +β Ξ΄[4]β ββ (β(2))/(4)Ξ΄[3]β =β β ββ 0.0625 β h[5]β =β (β(2))/(2)h[4]β ββ (1)/(4)h[3]β +β Ξ΄[5]β ββ (β(2))/(4)Ξ΄[4]β =β β ββ 0.0221 β h[6]β =β (β(2))/(2)h[5]β ββ (1)/(4)h[4]β +β Ξ΄[6]β ββ (β(2))/(4)Ξ΄[5]β =β 0
-
Respuesta al escalΓ³n mediante convoluciΓ³ny[n]β =β h[n]βx[n] β x[n]β =β u[n] β y[n]β =β ββ0.5ncosββ(Οn)/(4)ββ ββ u[n] β y[n]β =β βββ ββ βββ0.5kcosββ(Οk)/(4)ββ u[k]u[nβ ββ k]ββ β u[nβ ββ k]β =β β§β¨β© 1 kβ β€β n β β 0 kβ >β n u[nβ ββ k]β =β β§β¨β© 1 kβ β₯β 0 β β 0 kβ <β 0 β y[n]β =β βnkβ =β 00.5kcosββ(Οk)/(4)ββ Β β peroΒ cosββ(Οk)/(4)ββ β =β (1)/(2)e(jΟk)/(4)β +β (1)/(2)eβ ββ (jΟk)/(4) β β΄y[n]β =β βnkβ =β 0(0.5)kββ(1)/(2)e(jΟk)/(4)β +β (1)/(2)eβ ββ (jΟk)/(4)ββ
y[n]β =β βnkβ =β 0ββ(1)/(2)ββ ββ(1)/(2)e(jΟ)/(4)ββ kβ +β βnkβ =β 0ββ(1)/(2)ββ ββ(1)/(2)eβ ββ (jΟ)/(4)ββ k β y[n]β =β ββ(1)/(2)ββ βnkβ =β 0ββ(1)/(2)e(jΟ)/(4)ββ kβ +β ββ(1)/(2)ββ βnkβ =β 0ββ(1)/(2)eβ ββ (jΟ)/(4)ββ k β y[n]β =β ββ(1)/(2)ββ β‘β’β’β£(1β ββ ββ(1)/(2)e(jΟ)/(4)ββ nβ +β 1)/(1β ββ ββ(1)/(2)e(jΟ)/(4)ββ )β +β (1β ββ ββ(1)/(2)eβ ββ (jΟ)/(4)ββ nβ +β 1)/(1β ββ ββ(1)/(2)eβ ββ (jΟ)/(4)ββ )β€β₯β₯β¦u[n]
- Obtenga H(z), el diagrama de polos y ceros y decir si es o no estable el sistema.
- Determine el diagrama de bloques.
- Obtenga los primeros 5 valores de h[n] mediante recursividad.
SoluciΓ³n
-
H(z)β =β Ξ±ncos(Οn)βΊ(1β ββ Ξ±cos(Ο)zβ ββ 1)/(1β ββ 2Ξ±cos(Ο)zβ ββ 1β +β Ξ±2zβ ββ 2)H(z)β =β (1β ββ 0.5cosββ(Ο)/(4)ββ zβ ββ 1)/(1β ββ cosββ(Ο)/(4)ββ zβ ββ 1β +β 0.25zβ ββ 2) β H(z)β =β (1β ββ (β(2))/(4)zβ ββ 1)/(1β ββ (β(2))/(2)zβ ββ 1β +β (1)/(4)zβ ββ 2) β H(z)β =β (4β ββ β(2)zβ ββ 1)/(4β ββ 2β(2)zβ ββ 1β +β zβ ββ 2) β AsΓ,Β H(z)β =β (4z2β ββ β(2)z)/(4z2β ββ 2β(2)zβ +β 1)Se puede conocer entonces los polos y ceros4z2β ββ 2β(2)β +β 1β ββ z1β =β ((1)/(2)β ββ (i)/(2))/(β(2)),β Β z2β =β ((1)/(2)β +β (i)/(2))/(β(2)).Ceros: c1β =β 0,β Β c2β =β (1)/(2β(2)).Se puede notar de la grΓ‘fica que, al caer todos los puntos dentro del cΓrculo unitario, el sistema es estable.
% Ejercicio 6 a=[1 -sqrt(2)/4 0]; b=[1 -sqrt(2)/2 1/4]; zplane(b,a); ylabel(βEje imaginarioβ); xlabel(βEje real β); title(βDiagrama de polos y ceros del sistemaβ);
-
Diagrama de bloques del sistema.X(z)(β ββ β(2)zβ +β 4z2)β +β Y(z)(β ββ 4z2β +β 2β(2)z)β =β Y(z) β X(z)(β ββ β(2)zβ +β 4z2)β +β β ββ 4z2Y(z)β +β 2β(2)zY(z)β =β Y(z) β X(z)(β ββ β(2)zβ +β 4z2)β =β Y(z)β +β 4z2Y(z)β ββ 2β(2)zY(z) β X(z)(β ββ β(2)zβ +β 4z2)β =β Y(z)(4z2β ββ 2β(2)zβ +β 1) β H(z)β =β (Y(z))/(X(z))β =β (4z2β ββ β(2)z)/(4z2β ββ 2β(2)zβ +β 1) β H(z)β =β (z2β ββ (β(2))/(4)z)/(z2β ββ (β(2))/(2)β +β (1)/(4))
-
Por recursividad.y[n]β ββ (β(2))/(2)y[nβ ββ 1]β +β y[nβ ββ 2]β =β 4x[n]β ββ β(2)x[nβ ββ 1] β SiΒ x[n]β =β Ξ΄[n] β h[0]β =β (β(2))/(2)h[β ββ 1]β ββ h[β ββ 2]β +β 4Ξ΄[0]β ββ β(2)Ξ΄[β ββ 1]β =β 4 β h[1]β =β (β(2))/(2)h[0]β ββ h[β ββ 1]β +β 4Ξ΄[1]β ββ β(2)Ξ΄[0]β =β β(2) β h[2]β =β (β(2))/(2)h[1]β ββ h[0]β +β 4Ξ΄[2]β ββ β(2)Ξ΄[1]β =β β ββ 3 β h[3]β =β (β(2))/(2)h[2]β ββ h[1]β +β 4Ξ΄[3]β ββ β(2)Ξ΄[2]β =β β ββ (5β(2))/(2)
Análisis de Fourier de TC:
En los ejemplos con soluciΓ³n de esta secciΓ³n se abordan conceptos como la representaciΓ³n de seΓ±ales en serie de Fourier, comportamiento y respuesta de sistemas en el dominio de la frecuencia, correspondiente a la transformada de Fourier, asΓ como su representaciΓ³n grΓ‘fica.
Selecciona la dificultad en las caritas de la izquierda.
Análisis de Fourier de TC nivel principiante:
-
Considere la respuesta al impulso de un sistema comoSi la entrada es una exponencial compleja con Ο0β =β 2Determine el valor propio del sistema a la frecuencia de la seΓ±al de entrada.SoluciΓ³nUna forma de determinar el valor propio es a partir de la respuesta al impulso, h(t), para obtener funciΓ³n de transferencia evaluada a la frecuencia de la seΓ±al de entrada, es decir, que se puede obtener la funciΓ³n del sistema mediante la tΓ©cnica de Laplace unilateral y evaluarla a la frecuencia deseada. Esto esen donde
-
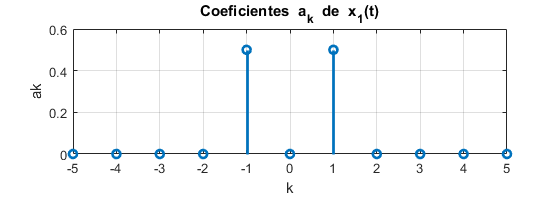
Exprese la seΓ±al x(t), con frecuencia fundamental Ο1, en forma exponencial,
como en la Ec. 5.1, y determine sus coeficientes ak.
c) β Verifique con Matlab los resultados y grafique para cada seΓ±al el diagrama espectral de los coeficientes ak vs k.
SoluciΓ³n
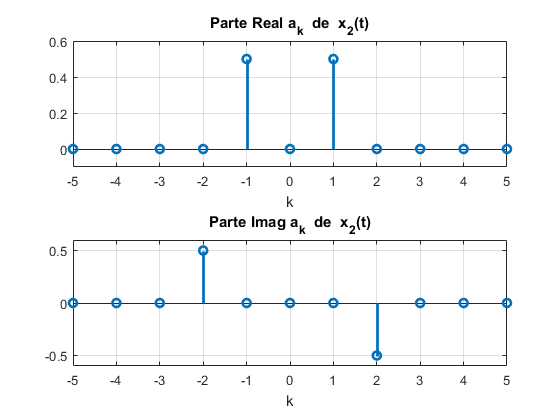
a) La seΓ±al x1(t) se puede expresar en tΓ©rminos de exponenciales complejas quedando en la forma de la Ec. 5.1 comoya que la frecuencia fundamental es Ο1, entonces y los coeficientes ak de las exponenciales se obtienen de manera directa comob) La seΓ±al x2(t) en este caso queda en tΓ©rminos de exponenciales complejas comoya que la frecuencia fundamental de x2(t) es Ο1, los coeficientes ak sonyc) En la figura inferior (5.1) se muestra la grΓ‘fica de los coeficientes de la seΓ±al x1(t), se observa que estΓ‘n presentes en que corresponden al coseno. En la figura (5.2) se muestra la grΓ‘fica de los coeficientes de la seΓ±al x2(t), se observa que la parte real a corresponde a un coseno a la frecuencia Ο0, mientras que la parte imaginaria corresponde a un seno a la frecuencia 2Ο0.
El cΓ³digo para obtener los coeficientes y la grΓ‘fica de x2(t) es%senal x2(t) wo=2*pi; T=1; t=0:0.001:T-0.001; x=cos(wo*t)+ sin(2*wo*t); %Grafica del espectro de x(t) ak=(1/length(t))*fft(x); %calculo de los coeficientes ak ak1=fftshift(ak); %calculo de los coeficientes ak con k=0 centrada k2=(length(ak1)/2)+1; k1=-5:5; d=5; β subplot(211),stem(k1,real(ak1(k2-d:k2+d)), βLineWidthβ,2); grid;title(βParte Real{ a}_{k } de {{ x}_{2}(t)}β);xlabel(βkβ);%ylabel(βakβ);% coeficientes ak axis([-5 5 -.1 .6]) β subplot(212), stem(k1,imag(ak1(k2-d:k2+d)), βLineWidthβ,2); grid;xlabel(βkβ);title(βParte Imag{ a}_{k } de {{ x}_{2}(t)}β);% angulos de ak axis([-5 5 -.6 .6])
Análisis de Fourier de TC nivel intermedio:
-
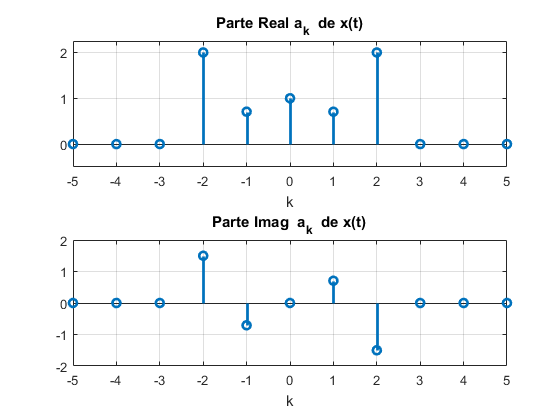
Exprese la seΓ±al x(t) en tΓ©rminos de exponenciales complejas, considerando que Ο2β
=β
2Ο1 y determine los coeficientes ak de la serie exponencial,
la Ec. 5.1 y grafique la parte real y la parte imaginaria.SoluciΓ³nx(t) se puede expresar en forma exponencial comoEn este caso los coeficientes de las exponenciales sonObserve que el subΓndice k de los coeficientes corresponde al mΓΊltiplo de la frecuencia fundamental. La figura (5.3) muestra la grΓ‘fica de los coeficientes.
-
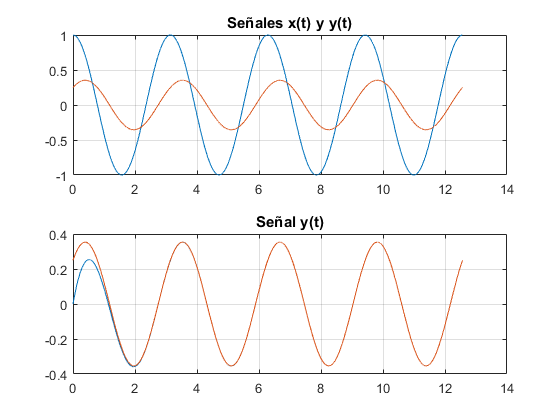
Considerando el ejemplo 1 en donde la respuesta al impulso corresponde a un sistema de primer orden, cuyo modelo, que relaciona la entrada con la salida esDetermine la respuesta del sistema a la entrada en dondeSoluciΓ³nDe acuerdo con la caracterΓstica de las funciones propias, la respuesta se obtiene de la Ec. 5.4, en la cual se requiere determinar el valor propio que se interpreta como la funciΓ³n del sistema evaluada a la frecuencia de la seΓ±al de entrada jΟ0.Del ejemplo 1, se obtuvoLa respuesta permanente y(t) con kβ =β 1, a1β =β 1, ya que sΓ³lo se tiene una exponencial, por lo queComo se observa en la resuesta y(t), Ec. 5.5, si una seΓ±al periΓ³dica se expresa en tΓ©rminos de exponenciales complejas, la respuesta del sistema sigue siendo la misma seΓ±al de entrada alterada en su magnitud y fase por el valor propio .
En la figura 5.4 se presenta en la grΓ‘fica superior las seΓ±ales traslapadas de entrada x(t) y de salida y(t), en donde la salida estΓ‘ atenuada en un factor de y con un atraso de β ββ Οβ ββ 4. La grΓ‘fica inferior corresponde a la salida y(t) de la Ec. 5.5, junto con la obtenida con Matlab con la funciΓ³n lsim() para su verificaciΓ³n, la cual muestra la parte transitoria.
Análisis de Fourier de TC nivel avanzado:
-
Se considera ahora el sistema de segundo orden dado porSi la entrada x(t) es del tipo sinusoidal, determine la respuesta del sistema a esta entrada.SoluciΓ³n
Los coeficientes espectrales se obtienen al expresar x(t) en forma exponencial, resultandoEl valor propio se obtiene con la funciΓ³n de transferencia de la Ec. 5.6que al sustituir sβ =β jΟ se obtiene la funciΓ³n del sistema en el dominio de la frecuencia, llamada Respuesta en Frecuencia.A partir de la cual se calcula el valor propio considerando la frecuencia de la seΓ±al de entrada Ο0β =β 1 y con kβ =β β ββ 1 y kβ =β 1De manera que la respuesta permanente y(t) esObteniendo finalmenteObserve que la respuesta y(t) se puede obtener de manera directa multiplicando y sumando la magnitud y el Γ‘ngulo, respectivamente, del valor propio con la entrada del sistema.
Análisis de Fourier en TD:
En los ejemplos con soluciΓ³n de esta secciΓ³n se abordan conceptos como la representaciΓ³n de seΓ±ales en serie de Fourier, comportamiento y respuesta de sistemas en el dominio de la frecuencia, correspondiente a la transformada de Fourier, asΓ como su representaciΓ³n grΓ‘fica.
Selecciona la dificultad en las caritas de la izquierda.
Análisis de Fourier en TD: nivel principiante:
Sistema de IdentificaciΓ³n de frecuencias de la seΓ±al x[n].
En esta actividad se identifican las frecuencias que componen una seΓ±al x[n]. ReafirmarΓ‘ los conceptos de Serie de Fourier, funciΓ³n de transferencia, transformada de Fourier, respuesta en frecuencia, filtro en TD.
El diagrama de bloques del sistema de detecciΓ³n de frecuencia se muestra en la Figura 6.3.
- Analice cuidadosamente el digrama de bloques para comprender la funcionalidad.
Análisis de Fourier en TD: nivel intermedio:
El programa descrito en el ejercicio anterior se compone de tres partes:
- GeneraciΓ³n de seΓ±al
- IdentificaciΓ³n de la primera frecuencia
- IdentificaciΓ³n de la segunda frecuencia
- Transcriba y ejecute el programa.
- Analice el programa e identifique la funcionalidad de acuerdo con el digrama de bloques de la Figura 6.3.
n=0:7; %Periodo de la seΓ±al de seΓ±al de 2 frecuencias x1=cos(pi*n/4)+cos(3*pi*n/4); %seΓ±al de 2 frecuencias yf1=1./(length(n))*fft(x1); %Espectro de seΓ±al de 2 frecuencias k=n; stem(k,yf1(k+1)) %Grafica de Espectro de seΓ±al de 2 frecuencias β %Identifica 1a frecuencia [b,a]=butter(2,3/8); %selecciΓ³n de filtro [H,w]=freqz(b,a); % Respuesta en frecuencia del filtro hold on plot(w,abs(H)); grid % Grafica de Respuesta en frecuencia del filtro yf11=filter(b,a,x1); % Respuesta a la salida del filtro yf12=(1./length(n))*fft(yf11); % Espectro de la seΓ±al filtrada figure stem(k,abs(yf1(k+1))) % Espectro de la seΓ±al x[n] β [m1 i1]=max(abs(yf12)) % Valor mΓ‘ximo del espectro de seΓ±al filtrada disp(βla frecuencia 1 es 2pi por:β) frecuencia=(pi./length(n))*(i1-1); %IdentificaciΓ³n de frecuencia rats((1./length(n)).*(i1-1)) β %Identifica 2a frecuencia Se repite para una segunda frecuencia [b1,a1]=butter(2,5/8,βhighβ); [H1,w]=freqz(b1,a1); hold on plot(w,abs(H1)); grid yf21=filter(b1,a1,x1); yf22=(1./length(n))*fft(yf21); β [m2 i2]=max(abs(yf22)) disp(βla frecuencia 2 es 2pi por:β) frecuencia=(pi./length(n))*(i1-1); rats((1./length(n)).*(i1-1))
Análisis de Fourier en TD: nivel avanzado:
Con base en el programa y Figuras generadas responda las siguientes preguntas.
- ΒΏQue representa la seΓ±al de TD de la Figura 1?
- ΒΏQue representa la seΓ±al de TC de la Figura 1 y de la Figura 2?
- Reconstruya la seΓ±al x[n] y grafΓquela.
- ΒΏEn que intervalo de frecuencias se encuentran las seΓ±ales de TD?
- ΒΏQue es un filtro?
- ΒΏQue tipo de filtros se estΓ‘n utilizando?
- ΒΏCual es la frecuencia de corte de la Figura 1 y de la Figura 2?
- Proponga una nueva frecuencia de corte para la seΓ±al de la Figura 2, de manera que no permita el paso de la primera armΓ³nica.
-
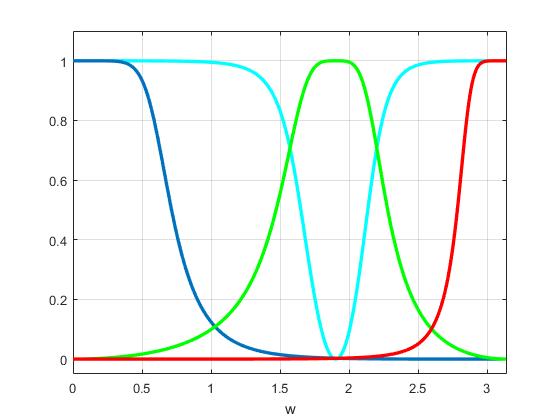
La Figura 6.4 incluye la respuesta en frecuencia de cuatro tipos de filtros.
- ΒΏComo se identifican y nombran a cada uno?
- ΒΏCual es la frecuencia de corte de cada uno, aproximadamente?