- Sistemas TC y TD
- Se√Īales TC y TD
- SLIT TC
- SLIT TD
- Fourier TC
- Fourier TD
Selecciona un tema de arriba.
Primero selecciona un tema de arriba.
Señales en TC y en TD:
En esta secci√≥n de Se√Īales TC y TD se presentan aplicaciones en las que el estudiante se familiariza con se√Īales pr√°cticas, de manera espec√≠fica con se√Īales de audio generadas de diversos dispositivos, las asocia e identifica de forma aproximada a modelos matem√°ticos.
Selecciona la dificultad en las caritas de la izquierda.
Señales en TC y en TD nivel principiante:
- "Guitarra.wav"
- "descolgado.wav"
1)
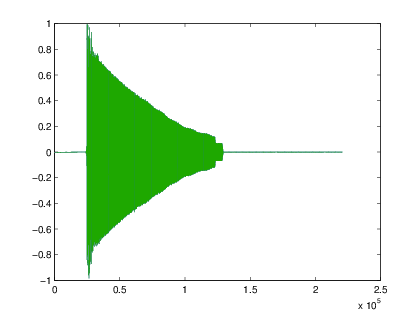
% sonido.m ’Guitarra.wav’,’descolgado.wav’
[y,fs]=wavread(’Guitarra.wav’);
sound(y,fs);
plot(y)
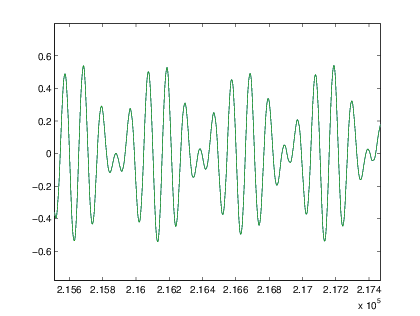
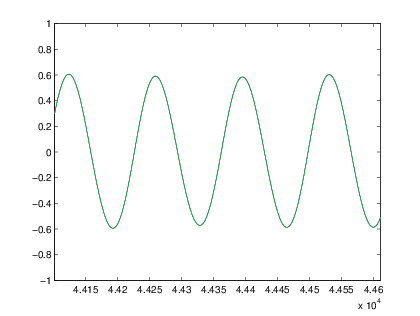
%sonido.m ’Guitarra.wav’,’descolgado.wav’
[y,fs]=wavread(’descolgado.wav’);
sound(y,fs);
plot(y)
Se identifica que son dos se√Īales cotidianas, la nota de una guitarra y el sonido de descolgado del tel√©fono; adem√°s se observa que la se√Īal de ‚ÄôGuitarra.wav‚Äô es una se√Īal senoidal cuya amplitud decae exponencialmente, mientras que ‚Äôdescolgado.wav‚Äô corresponde a la multiplicaci√≥n de dos senoidales, una de baja frecuencia y otra de alta frecuencia. Adem√°s, se identifica que estos dos sonidos reales pueden representarse, de forma muy aproximada, mediante funciones matem√°ticas, senos y cosenos.
Señales en TC y en TD nivel intermedio:
-
Grabe las se√Īales de audio que se enlistan. La funci√≥n wavread permite leer un archivo de sonido tipo ‚Äô*.wav‚Äô (Read Microsoft Wave). Utilice dicha funci√≥n para leer archivos de sonido indicados. Con la funci√≥n sound se podr√° reproducir el sonido. Adem√°s, grafique la se√Īal de sonido, y con la herramienta de amplificar (Zoom in ) observe e identifique el tipo de se√Īal.
- Un silbido sostenido lo m√°s posible.
- El tintineo de una campana.
- El sonido de un diapasón.
- La nota de alg√ļn instrumento musical: piano, flauta, etc.
- El sonido de un martillo neum√°tico.
- El golpe de un bat a una pelota.
Señales en TC y en TD nivel avanzado:
- Investigue el valor de la divisa del dolar americano, a la venta, en los √ļltimos 30 d√≠as. Con los datos obtenidos, grafique la se√Īal e identifique si la se√Īal es de tiempo continuo o discreto, determin√≠stica o aleatoria, peri√≥dica o aperi√≥dica, de energ√≠a o de potencia. Considere que los d√≠as en que no haya movimiento econ√≥mico, el valor de la divisa ser√° el del d√≠a anterior.
Sistemas LIT en TC y en TD:
En esta secci√≥n de Sistemas TC y TD se presentan actividades que permiten a los estudiantes ejercitarse intensamente sobre los temas, se generan aplicaciones que tengan sentido para ellos y que les son √ļtiles a lo largo de su carrera.
Selecciona la dificultad en las caritas de la izquierda.
Sistemas LIT en TC y en TD nivel principiante:
Sistemas LIT en TC y en TD nivel intermedio:
Sistemas LIT en TC y en TD nivel avanzado:
Ventaja de la linealidad en los sistemas:
Hay ciertos sistemas lineales, para los cuales, es posible reducir el costo de ejecuci√≥n al utilizar la linealidad del sistema. De esta forma, si en dicho sistema se deben sumar varias se√Īales de salida, vale la pena investigar si es posible eficientar el proceso al sumar primero las se√Īales de entrada. El siguiente ejercicio ilustra esta situaci√≥n.
Suponga que se tiene una base de datos de la temperatura promedio de cada d√≠a, de cierta localidad, por los √ļltimos 100 a√Īos. De esta forma, se desea obtener el promedio, durante esos 100 a√Īos, de la temperatura de cada d√≠a del a√Īo. Dicho proceso es sencillo; sin embargo, al consultar la base de datos, se observa que existen algunos d√≠as en donde la tempera es considerablemente distinta respecto a las temperaturas de los d√≠as cercanos a estos; por ejemplo: la temperatura del 21 de mayo de 1983 fue de 7¬įC, mientras que en los d√≠as 19, 20, 22 y 23 de mayo de ese mismo a√Īo, las temperaturas fueron de 16¬į, 14¬į, 14.5¬į y 15¬į respectivamente; por lo cual, se desea suavizar la base de datos promediando la temperatura de cada d√≠a con respecto a las temperaturas registradas 2 d√≠as antes y dos d√≠as despu√©s (sistema promedio m√≥vil).
Una manera de hacer el proceso es aplicar el sistema promedio m√≥vil a cada una de las se√Īales que representa la temperatura de cada d√≠a del a√Īo y, posteriormente, promediar las se√Īales de salida; se puede observar que en este enfoque el sistema promedio m√≥vil tendr√≠a que ejecutarse para 100 se√Īales distintas (una por cada a√Īo).
Una forma alterna de abordar el problema, es haciendo uso de la linealidad del sistema promedio m√≥vil, lo que implicar√≠a primero promediar las se√Īales de temperatura de los 100 a√Īos y, posteriormente, introducir al sistema la suma de estas se√Īales. En este caso s√≥lo se tendr√≠a que ejecutar en una ocasi√≥n al sistema promedio m√≥vil.
Para verificar que el sistema se ejecuta más rápido en la segunda metodología, realice dos programas en Matlab que reproduzcan el sistema descrito anteriormente con cada una de las metodologías propuestas.
Notas:
- Para medir el tiempo de ejecución, puede utilizar el par de funciones de Matlab, tic y toc.
- Observe que el sistema se indetermina para los valores de n‚ÄÖ=‚ÄÖ1,‚ÄÖ2,‚ÄÖ364 y 365, ya que requerir√≠a de x[‚ÄÖ‚ąí‚ÄÖ1], x[0], x[366] y x[367]. De esta forma, suponga que y[1]‚ÄÖ=‚ÄÖ0, y[2]‚ÄÖ=‚ÄÖ0, y[364]‚ÄÖ=‚ÄÖ0 y y[365].
-
Para obtener la base de datos de la temperatura diaria por un lapso de 100 a√Īos, genere una pseudo base de datos con ayuda de la funci√≥n de Matlab randi; que genera una matriz A de tama√Īo NxM de n√ļmeros enteros pseudo‚Äďaleatorios en un dominio de [numMin,numMax]. Para el ejercicio M‚ÄÖ=‚ÄÖ365, N‚ÄÖ=‚ÄÖ100, y se propuso que la temperatura m√≠nima de la base de datos (numMin) es de 13¬į, mientras que, la temperatura m√°xima (numMax) es de 38¬į; esto es:Por √ļltimo, no se considera que existan a√Īos bisiestos en la base de datos.
A=randi([13,38],365,100)
Programa para realizar el proceso seg√ļn la primera metodolog√≠a:
Código en matlab:
A=randi([13,38],365,100);
‚Äč
% --> y_is Es una matriz que por columna registra el promedio móvil de las
%temperaturas diarias por un a√Īo
‚Äč
%--------------------------------------------%
%reservar memoria para y_is:
y_is = zeros(size(A));
‚Äč
%--------------------------------------------%
%inicializar el reloj para saber cu√°nto dura el proceso
tic
‚Äč
%--------------------------------------------%
%Sistema promedio móvil
for c1=1:1:100 %---> recorre a√Īo por a√Īo
for c2=3:1:363 %---> recorre día por día
y_is(c2,c1)=1/5*( A(c2-2,c1)+A(c2-1,c1)+A(c2,c1)+...
A(c2+1,c1)+A(c2+2,c1) );
end
end
‚Äč
%--------------------------------------------%
%Obtener la salida final del sistema, y[n], como el promedio de las
%temperaturas diarias
y=(1/N)*sum(y_is’);
‚Äč
%--------------------------------------------%
%detener el reloj
tiempo1=toc
‚Äč
%--------------------------------------------%
%recortar de y[n] los elementos 1,2,364,365
y([1,2,364,365])=[];
Programa para realizar el proceso seg√ļn la segunda metodolog√≠a:
Código en matlab:
A=randi([13,38],365,100);
‚Äč
%--------------------------------------------%
%reservar memoria para y_is:
y_is = zeros(size(A));
‚Äč
%--------------------------------------------%
%inicializar el reloj para saber cu√°nto dura el proceso
tic
‚Äč
%--------------------------------------------%
%Promediar las temperaturas diarias a trav√©s de todos los a√Īos
% ---> x[n]
x=(1/N)*sum(A’);
‚Äč
%--------------------------------------------%
%ingresar la se√Īal x[n] al sistema promedio m√≥vil
‚Äč
for c2=3:1:363 %---> recorre día por día
y(c2)=1/5*( x(c2-2)+x(c2-1)+x(c2)+...
x(c2+1)+x(c2+2) );
end
‚Äč
%--------------------------------------------%
%detener el reloj
tiempo2=toc
El tiempo de procesamiento del sistema, promedio m√≥vil, aplicado de acuerdo a la primera metodolog√≠a fue de 9.3639X10‚ÄÖ‚ąí‚ÄÖ04 segundos, mientras que el tiempo de procesamiento del sistema, promedio m√≥vil, aplicado de acuerdo a la segunda metodolog√≠a fue de 2.1137X10‚ÄÖ‚ąí‚ÄÖ04, esto es, el proceso en el que primero se promedi√≥ la temperatura de la base de datos y posteriormente se aplic√≥ el sistema promedio m√≥vil, fue 4.4 veces m√°s r√°pido que el proceso en el que primero se realiz√≥ el promedio m√≥vil a cada una de las 100 se√Īales y posteriormente se promediaron las se√Īales de salida.
Sistemas Lineales Invariantes en el Tiempo en TC:
En esta sección de SLIT TC se presentan aplicaciones prácticas para ser realizadas de forma simulada o bien en el laboratorio. Se incluyen sistemas eléctricos de primero y segundo orden.
Selecciona la dificultad en las caritas de la izquierda.
Sistemas Lineales Invariantes en el Tiempo en TC nivel principiante:
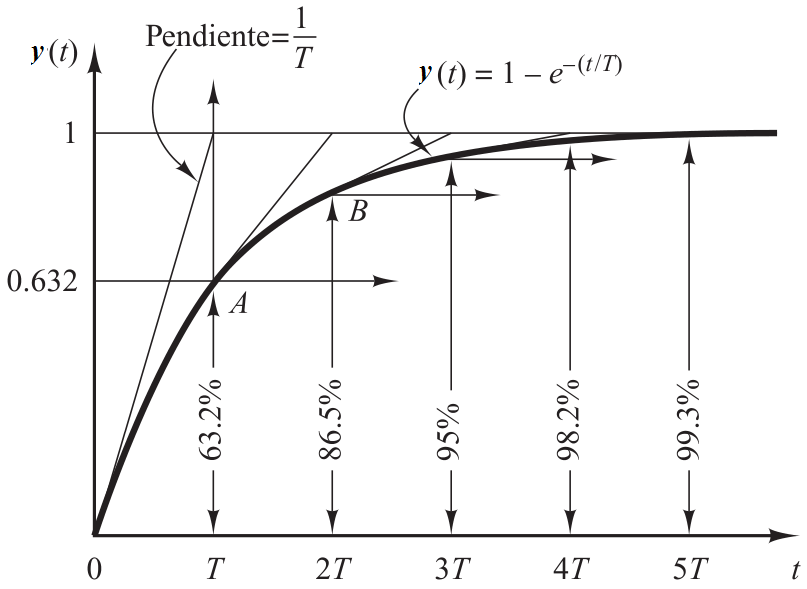
Teoría Básica
Sistema de 1er Orden
Función de Transferencia
Respuesta al escalón
Constante de tiempo
Cuestionario Previo
- La función de transferencia
- La respuesta al impulso
- La respuesta al escalón
- La constante de tiempo
- La función de transferencia
- La respuesta al impulso
- La respuesta al escalón
- La constante de tiempo
An√°lisis Experimental
Experimento 1
Experimento 2
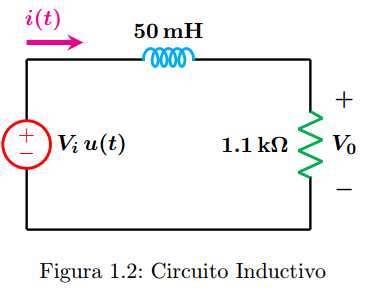
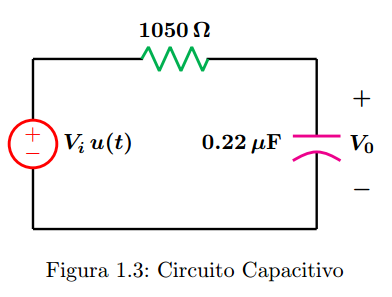
Sistemas Lineales Invariantes en el Tiempo en TC nivel intermedio:
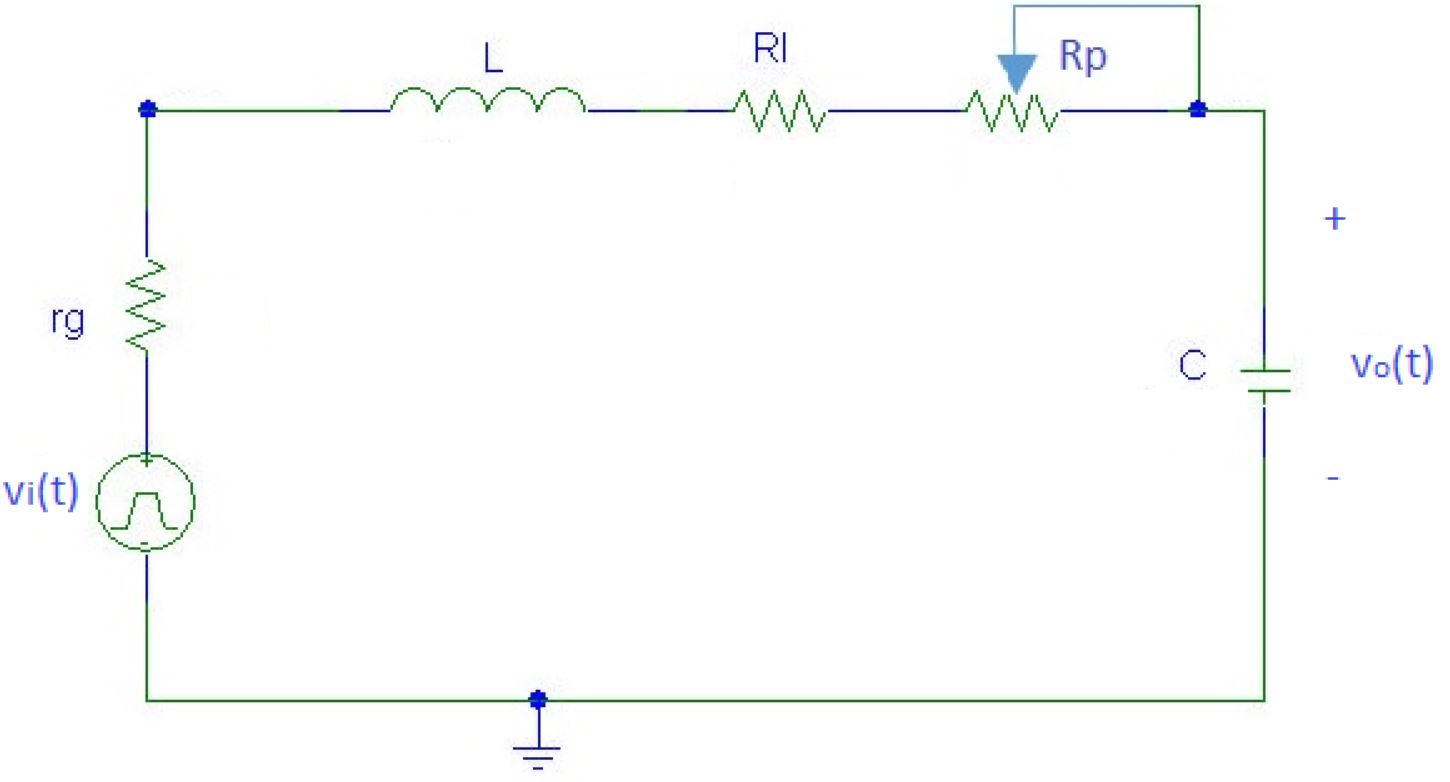
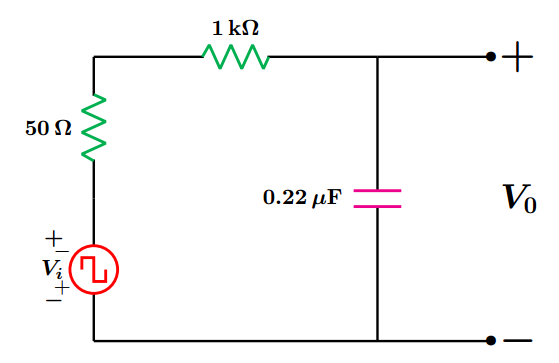
L es un inductor de 50mH
C es un capacitor de 0.22őľF
Re‚ÄÖ=‚ÄÖrg‚ÄÖ+‚ÄÖRl‚ÄÖ+‚ÄÖRp es la resistencia equivalente con los valores de 50 ő©, 50 ő© y 2000 ő©, respectivamente.
- Determine la función de transferencia del sistema (FTS).
- Identifique los coeficientes de la FTS con los de la Ec. 3.7 y exprese la frecuencia natural del sistema wn y la raz√≥n de amortiguamiento ő∂ en t√©rminos de Re,‚ÄÖ L,‚ÄÖ C .
- Con Rp‚ÄÖ=‚ÄÖ0 determine el valor de ő∂ y el de wn.
- Obtenga las raíces del sistema y dibuje el diagrama de polos y ceros.
- Determine y grafique la respuesta al impulso y diga que comportamiento tiene el sistema.
- Determine y grafique la respuesta al escalón.
- Con Rp‚ÄÖ=‚ÄÖ2000 ő©, m√°ximo valor, determine el valor de ő∂ y el de wn.
- Obtenga las raíces del sistema y dibuje el diagrama de polos y ceros.
- Determine y grafique la respuesta al impulso y diga que comportamiento tiene el sistema.
- Determine y grafique la respuesta al escalón.
- Determine el valor de Rp con el que se obtiene un comportamiento criticamente amortiguado.
- Obtenga las raíces del sistema y dibuje el diagrama de polos y ceros.
- Con ese valor determine y grafique la respuesta al impulso.
- Determine y grafique la respuesta al escalón.
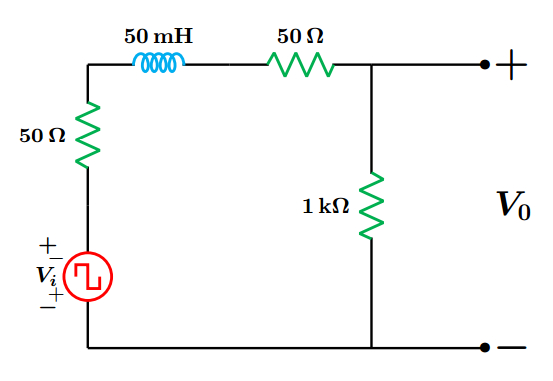
Sistemas Lineales Invariantes en el Tiempo en TC nivel avanzado:
Esta actividad es un ejercicio de aplicación práctica que requiere de equipo y accesorios:
- Osciloscopio
- Generador de formas de onda
- 1 potenci√≥metro de 2 kő©
- 1 capacitor cer√°mico de 0.22őľF a 25 V o mayor
- 1 inductor de 50mH.
- 6 cables caim√°n-caim√°n
- 6 cables banana-banana
- 6 cables banana-caim√°n
- 1 protoboard
- Genere una se√Īal cuadrada peri√≥dica con una frecuencia de 100Hz. esta se√Īal corresponde a una suma infinita de se√Īales escal√≥n.
-
Arme el circuito de la figura y alimente con la se√Īal cuadrada.

- Conecte un canal del osciloscopio en la entrada del circuito y otro canal en la salida.
-
Coloque el cursor del potenci√≥metro en el m√°ximo valor y observe en el osciloscopio la se√Īal de salida. Con base en la se√Īal observada:
- Obtenga una copia de la forma de onda experimental y compare la respuesta teórica con la respuesta experimental.
- Especifique como se le nombra a este comportamiento del sistema.
-
Con Rp‚ÄÖ=‚ÄÖ0 determine:
- Obtenga una copia de la forma de onda experimental y compare la respuesta teórica con la respuesta experimental.
- Especifique como se le nombra a este comportamiento del sistema.
- Varíe el valor del potenciómetro al valor encontrado en el punto 11 de la investigación previa, en el osciloscopio se observará, de manera aproximada, que la respuesta al escalón tiene un comportamiento criticamente amortiguado. Obtenga una copia de la forma de onda experimental y compare la respuesta teórica con la respuesta experimental.
- ¬ŅSe puede lograr de forma experimental observar el comportamiento oscilatorio? Justifique su respuesta.
Sistemas lineales e invariantes en el tiempo en TD:
En esta secci√≥n de SLIT TD se presentan aplicaciones pr√°cticas para la generaci√≥n y eliminaci√≥n de ecos. Se inicia con simulaciones sencillas, se avanza con el proceso de ecos en se√Īales de audio grabadas a trav√©s de sistemas FIR, posteriormente se procesan las se√Īales a mediante sistema IIR para eliminar los ecos y obtener la se√Īal original.
Selecciona la dificultad en las caritas de la izquierda.
Sistemas lineales e invariantes en el tiempo en TD nivel principiante:
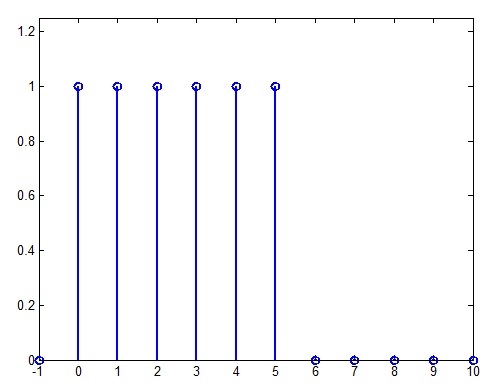
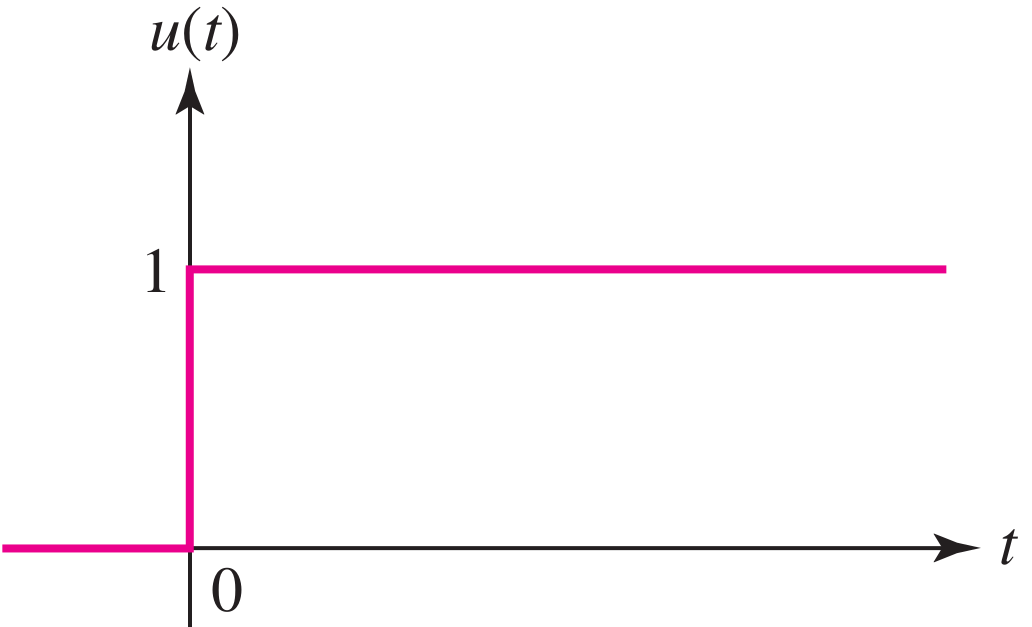
- Genere la se√Īal x[n]‚ÄÖ=‚ÄÖu[n]‚ÄÖ‚ąí‚ÄÖu[n‚ÄÖ‚ąí‚ÄÖ6] y graf√≠quela.
- Obtenga el modelo y la funci√≥n de transferencia del sistema FIR de la ec.1.1 Considere un solo eco con őĪ‚ÄÖ=‚ÄÖ0.5 y N‚ÄÖ=‚ÄÖ10.
- Obtenga la respuesta del sistema FIR a la entrada x[n] y grafíquela.
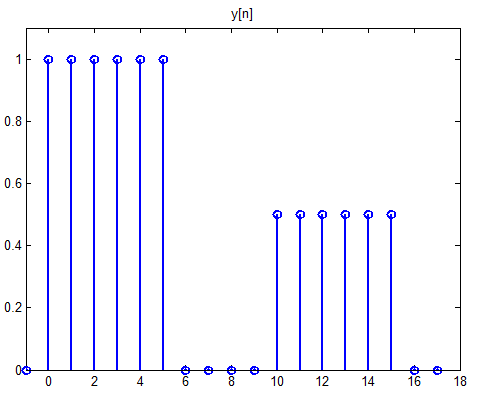
- Obtenga el modelo y la funci√≥n de transferencia del sistema IIR de la ec.1.2. Considere de nuevo őĪ‚ÄÖ=‚ÄÖ0.5 y N‚ÄÖ=‚ÄÖ10.
- Obtenga la respuesta del sistema IIR a la entrada y[n] y grafíquela.
- Verifique la generación y eliminación del eco.
-
-
La función de transferencia de H1(z) es:
-
La respuesta del sistema se obtiene multiplicando la función de tranferencia con la transformada Z de la entrada.
antitransformando Y(z) se llega aLa gr√°fica de la respuesta es
-
la función de transferencia de H2(z) es:
-
La entrada al sistema 2 es Y(z)
y la salida del sistema 2 es
De manera quela cual corresponde a la entrada.
- Se√Īal original y 3 ecos.
- Atenuación de ecos en donde k = 1:3.
- Desplazamiento N‚ÄÖ=‚ÄÖ6,‚ÄÖ8,‚ÄÖ10,‚ÄÖ12 .
- Obtenga las expresiones de las Funciones de Transferencia del los sistemas H1(z) y H2(z).
-
Utilice la función filter para obtener la respuesta de los sistemas.
- Obtenga las gr√°ficas de las se√Īales de entrada x[n], de la salida del sistema FIR y[n] y de la salida del sistema IIR w[n].
-
Con N‚ÄÖ=‚ÄÖ6
-
%Funci√≥n escal√≥n unitario function u=ud(n) u=+1.*(n>=0); ____________________________________________ % Generador y Eliminador de Ecos % Sistemas FIR-IIR en cascada % ecobase1.m GMata n=-1:37; len=length(n); N=6; %Desplazamiento x1=ud(n)-ud(n-6); %Se√Īal de entrada %Coeficientes de la FT del Sistema FIR a=1; b=[1 zeros(1,N-1) 0.5 zeros(1,N-1) 0.25 zeros(1,N-1) 0.125]; %Se√Īal salida Sistema FIR =Se√Īal de entrada Sistema IIR y1=filter(b,a,x1); ‚Äč a=[ 1 zeros(1,N-1) .5 zeros(1,N-1) 0.25 zeros(1,N-1) 0.125]; b=1; w=filter(b,a,y1); %%Se√Īal salida Sistema IIR ‚Äč subplot(311), stem(n,x1,‚ÄôLineWidth‚Äô,2);title(‚ÄôSe√Īal original:x[n]‚Äô); axis([-1 len 0 1.1]); subplot(312),stem(n,y1,‚ÄôLineWidth‚Äô,2); title(‚ÄôRespuesta Sistema FIR: y[n]‚Äô);axis([-1 len 0 1.1]); subplot(313),stem(n,w,‚ÄôLineWidth‚Äô,2); title(‚ÄôRespuesta Sistema IIR: w[n]‚Äô);axis([-1 len 0 1.1]);
-
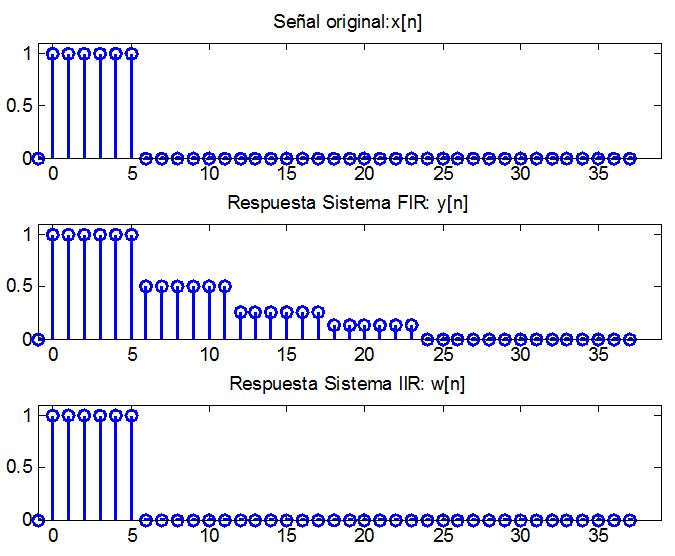
Sistemas lineales e invariantes en el tiempo en TD nivel intermedio:
Genere la se√Īal . Considere la frecuencia de la se√Īal f‚ÄÖ=‚ÄÖ261Hz, la frecuencia de muestreo Fs‚ÄÖ=‚ÄÖ4000Hz (pruebe tambien con Fs‚ÄÖ=‚ÄÖ6000Hz y Fs‚ÄÖ=‚ÄÖ8000Hz).
-
Considere 3 ecos con una atenuación de
en donde k = 1:3. Exprese la función de transferencia para este sistema.
-
Obtenga la respuesta del sistema FIR a la entrada x[n]. Utilice la funci√≥n filter. Grafique la se√Īal y verifique que la respuesta incluya la se√Īal original y los tres ecos.
-
Obtenga la respuesta del sistema IIR a la entrada y[n] y grafíquela, de manera que se anulen los tres ecos.
Sistemas lineales e invariantes en el tiempo en TD nivel avanzado:
-
Grabe una se√Īal de audio, por ejemplo su nombre, o bien, utilice la grabaci√≥n que se proporciona ‚Äôarroz.wav‚Äô.
-
Con la funci√≥n wavread lea el archivo de sonido e identifique los datos de la se√Īal y la frecuencia de muestreo con la que fue grabada.
-
Realice una función en Matlab, ecos(voz,Fs,ne,Nspa) que genere los ecos y que se reproduzcan en audio, en donde los parámetros de la función sean:
- voz: son los datos del archivo de sonido proporcionados con la función wavread,
- Fs: frecuencia de muestreo proporcionada con la función wavread,
- ne: n√ļmero de ecos a generar,
- Nspa: n√ļmero de espacios entre ecos.
Adem√°s se tendr√° que generar un vector de ceros con la funci√≥n zeros() de longitud Nspa, spa=zeros(1,Nspa), de manera que el vector y de la se√Īal a la salida del sistema FIR quede:
y=[voz spa eco1 spa eco2 spa eco3 spa ..... eco-ne ].
Utilice la funci√≥n sound() para reproducir la se√Īal con ecos contenida en el vector y. Inicie con Nspa =0.
- Grafique las se√Īales de voz, y1[n] y w[n]. Utilice la funci√≥n subplot(), stem ...
Serie de Fourier de TC:
En esta secci√≥n de Fourier TC se aplican los conceptos en se√Īales peri√≥dicas de TC para realizar un an√°lisis en el dominio de la frecuencia. Bajo este esquema se introduce el concepto de filtrado de se√Īales.
Tambi√©n, se incluye una aplicaci√≥n del an√°lisis de Fourier de una se√Īal card√≠aca bajo la consideraci√≥n de una se√Īal peri√≥dica.
Selecciona la dificultad en las caritas de la izquierda.
Serie de Fourier de TC nivel principiante:
-
-
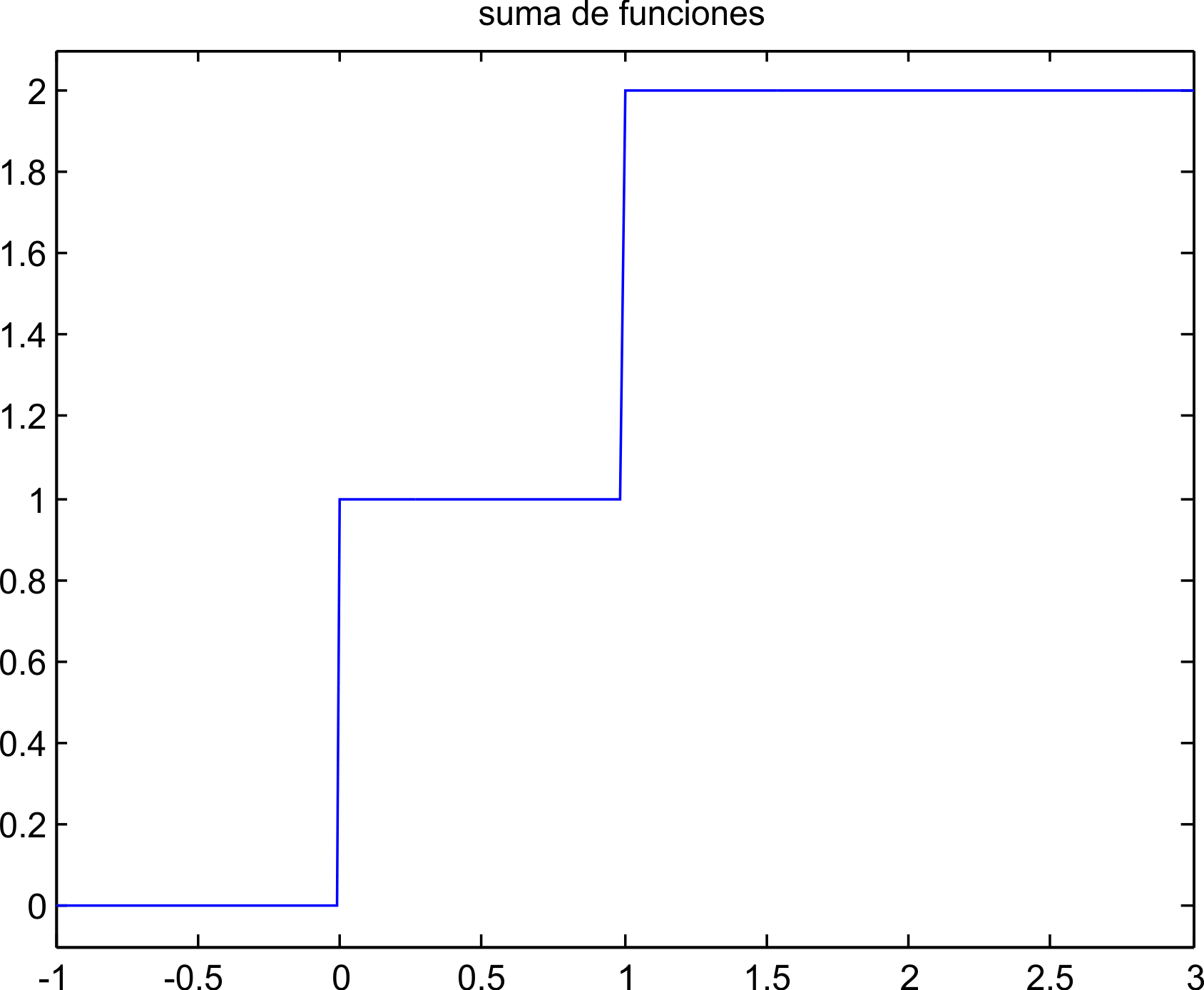
Considerando se√Īales continuas, se pueden sumar dos se√Īales escal√≥n cuyo inicio es en tiempos diferentes, por ejemplo la suma de un escal√≥n que inicie en el t‚ÄÖ=‚ÄÖ0 mas otro que inicia en t‚ÄÖ=‚ÄÖ1, es decir que (como se muestra en la figura 5.1)
t=-1:0.01:3; ‚Äč u=us(t)+us(t-1); plot(t,u); axis([-1 3 -.1 2.1]) title(‚Äôsuma de funciones‚Äô)
-
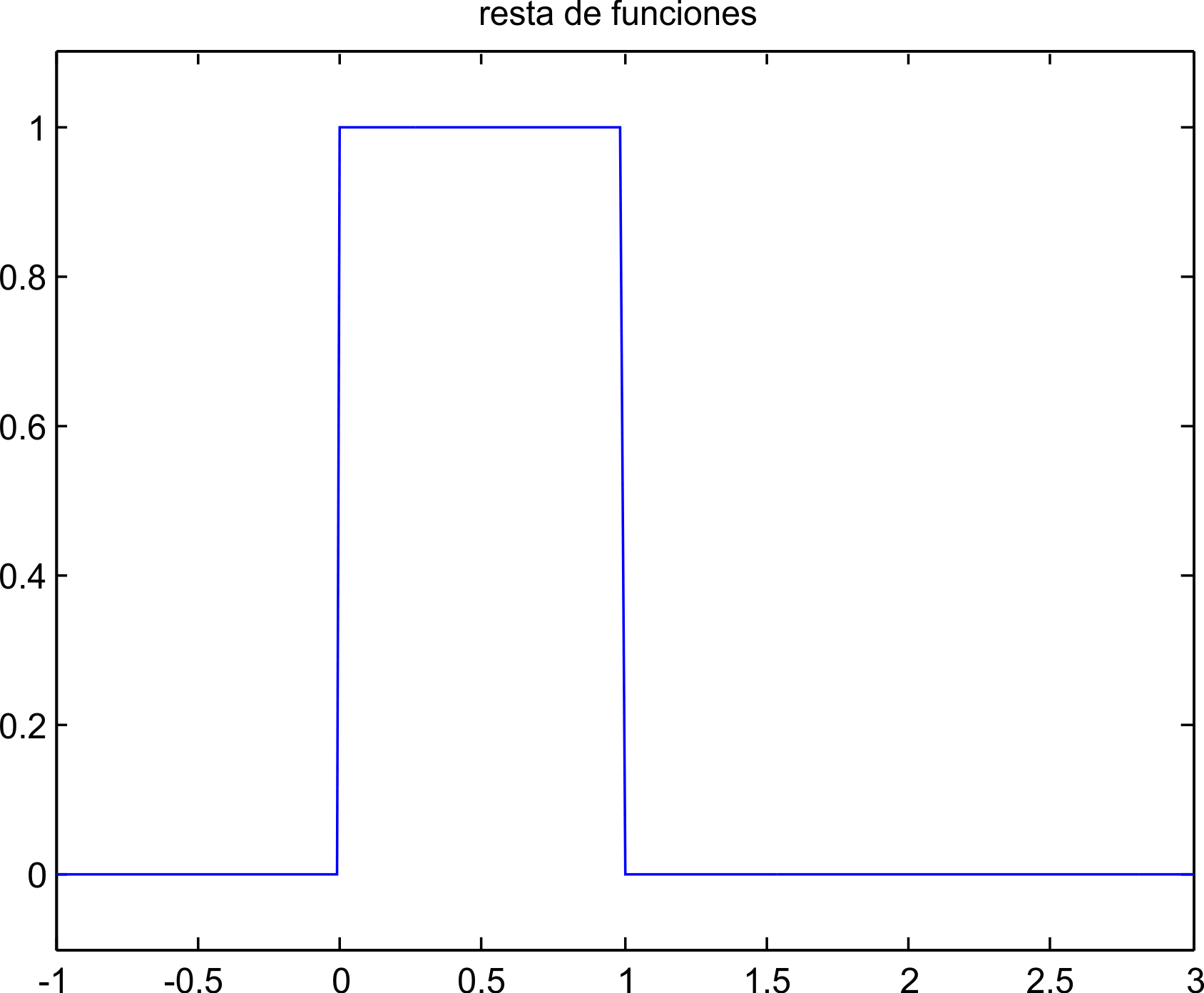
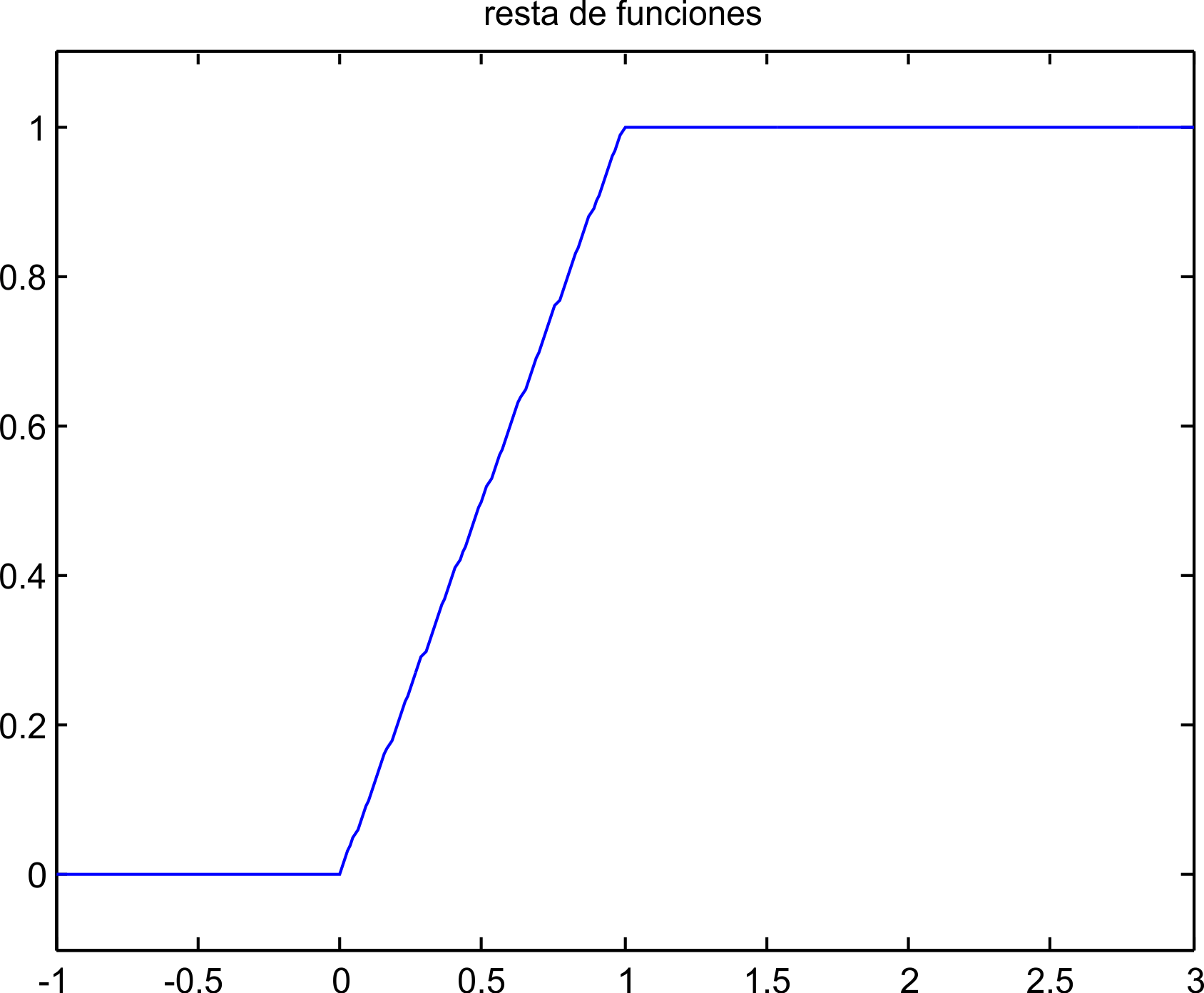
La resta de dos escalones en los tiempos establecidos en el ejemplo anterior, se tiene la expresión, mientras que la gráfica correspondiente se muestra en la figura 5.2.
t=-1:0.01:3; ‚Äč u=us(t)-us(t-1); plot(t,u); axis([-1 3 -.1 1.1]) title(‚Äôresta de funciones‚Äô)
-
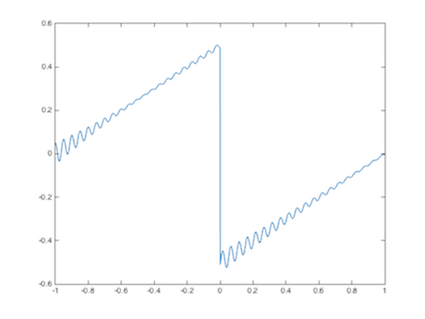
Se pueden sumar y restar rampas, por ejemplo se sumar√°n y restar√°n dos rampas las que respectivamente tienen inicio en t‚ÄÖ=‚ÄÖ0 y t‚ÄÖ=‚ÄÖ1
La suma de rampas se muestra en la figura 5.3, mientras que la resta en la figura 5.4
t=-1:0.01:3; ‚Äč u=rs(t)+rs(t-1); plot(t,u); axis([-1 3 -.1 2.1]) title(‚Äôsuma de funciones‚Äô) ‚Äč
t=-1:0.01:3; ‚Äč u=rs(t)-rs(t-1); plot(t,u); axis([-1 3 -.1 1.1]) title(‚Äôresta de funciones‚Äô)
-
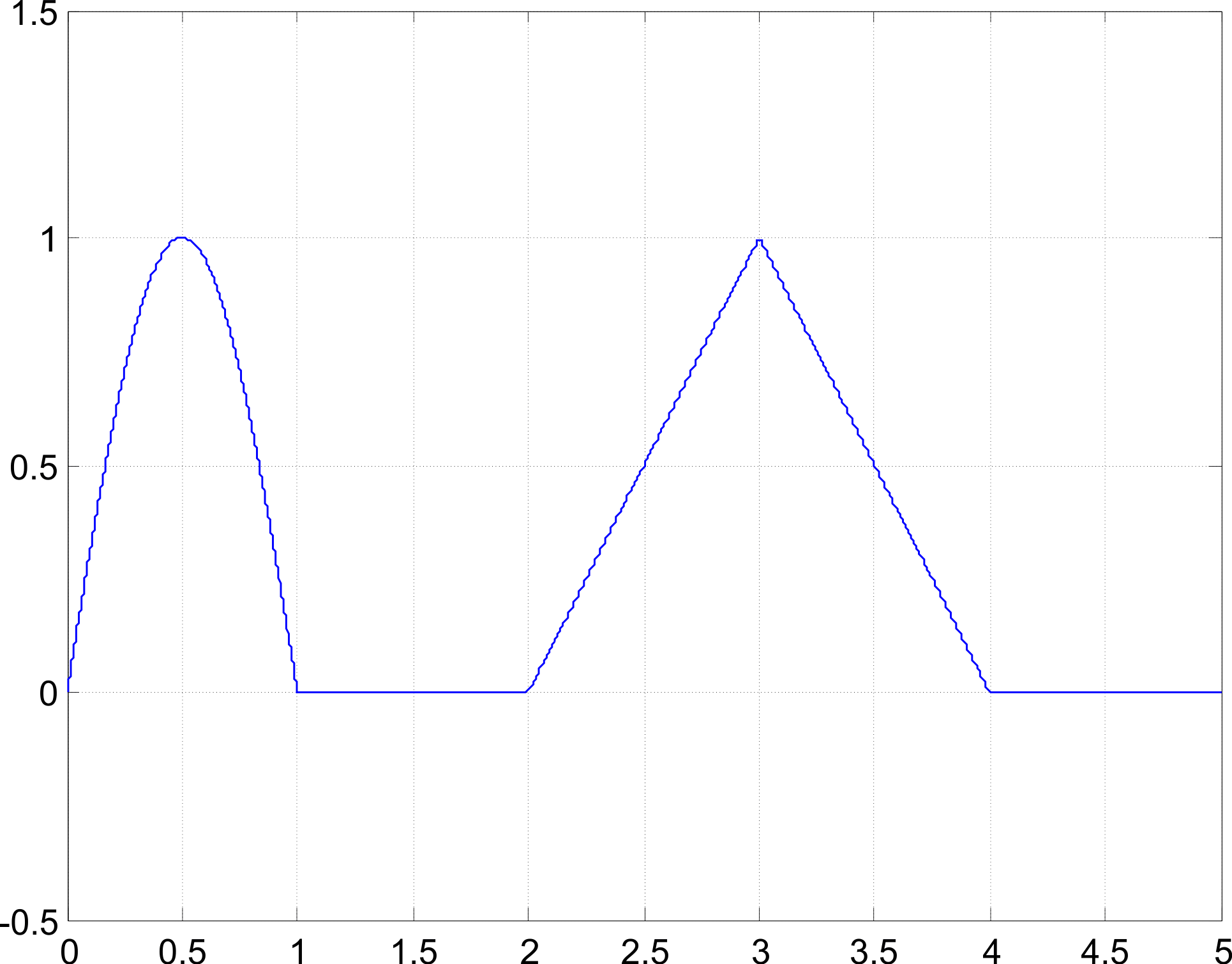
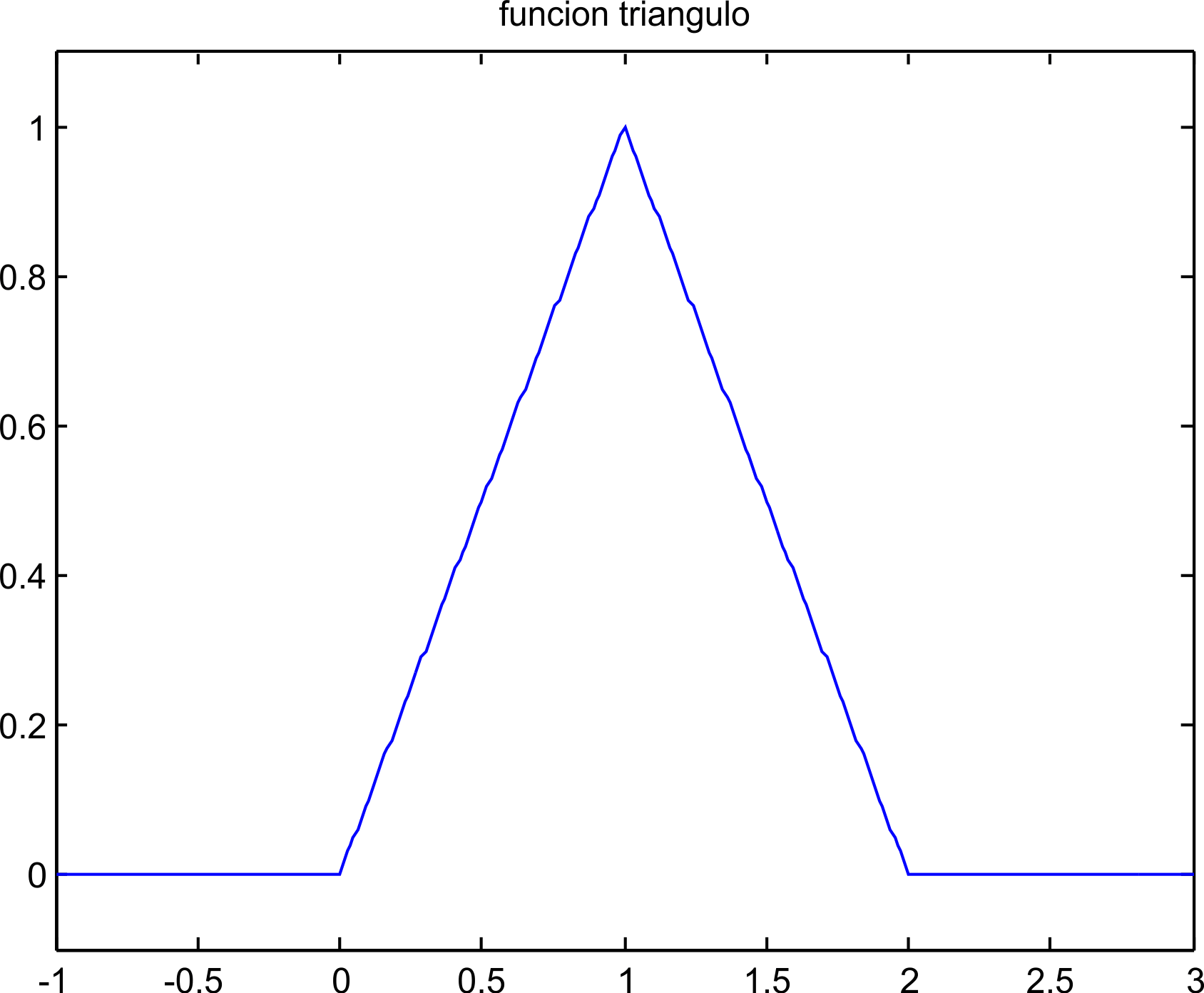
Una función con forma triangular se puede obtener a partir de la suma y resta de cuatro rampas, para tener la funcion triangular que se muestra en la figura 5.5, se puede expresar de la forma:
o bien
t=-1:0.01:3; ‚Äč u=rs(t)-2*rs(t-1)+rs(t-2); plot(t,u); axis([-1 3 -.1 1.1]) title(‚Äôfuncion triangulo‚Äô)
Serie de Fourier de TC nivel intermedio:
-
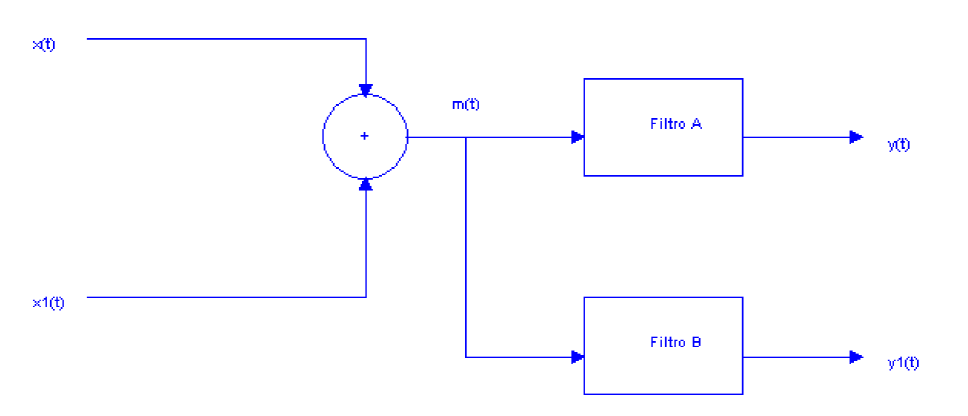
Considere el diagrama de bloques de la figura y las se√Īales x(t) y x1(t).
- Graficar x(t),‚ÄÖx1(t) y m(t).
- Obtener los coeficientes de la serie de Fourier deblas se√Īales x(t),‚ÄÖx1(t) y m(t).
- Graficar el espectro de x(t), x1(t) y m(t).
- Seleccionar y aplicar los filtros Butterwoth apropiados de manera que y(t)‚ÄÖ=‚ÄÖx(t) y y1(t)‚ÄÖ=‚ÄÖx1(t).
-
Preguntas de investigación y reflexión.
- En este ejercicio, los filtro seleccionados fueron de orden 6, pruebe el mismo ejercicio con filtros de orden 2 y 4 e identifique que diferencias existen.
- Compare la salida de ambos filtros con las correspondientes se√Īales de entrada e identifique que diferencia existe.
- Para los filtros de segundo orden, obtenidos con la función butter(), exprese la función de transferencia, el modelo en el dominio del tiempo y la expresión de la respuesta en frecuencia de cada filtro.
- Para cada uno de los filtros de segundo orden, grafique la respuesta en frecuencia en magnitud y √°ngulo.
- En las gr√°ficas de la respuesta en frecuencia de los filtros de orden 6, se ha presentado s√≥lo la magnitud y no se ha incluido el √°ngulo de fase. ¬ŅComo afecta el √°ngulo de fase del filtro en la se√Īal filtrada?
Solución
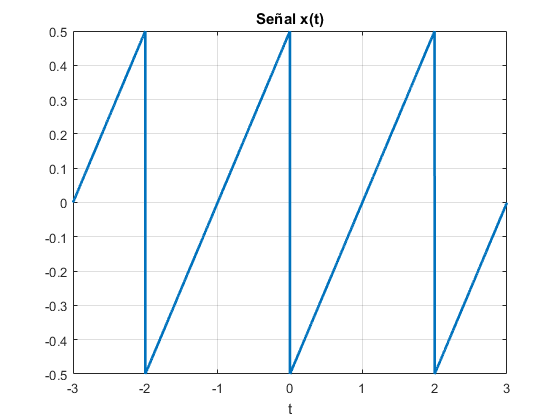
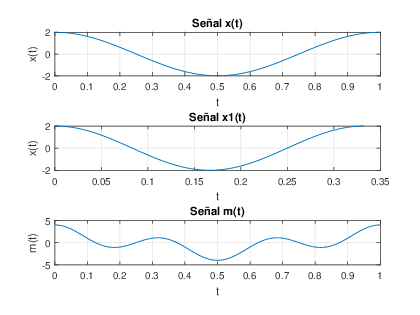
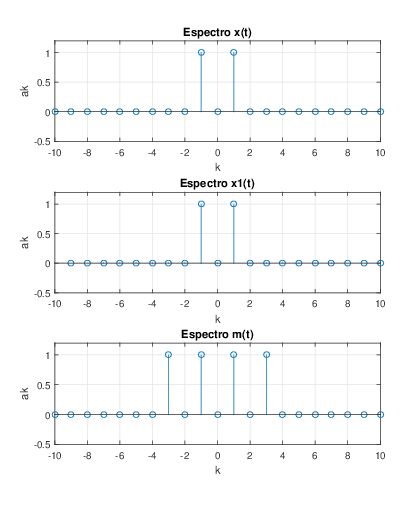
6. a) Para la generaci√≥n, simulaci√≥n y gr√°ficas de las se√Īales x(t),‚ÄÖx1(t) y m(t), mostradas en la figura. Se observa que el periodo de m(t) es T‚ÄÖ=‚ÄÖ1.%Senal x(t): wo=2*pi; % Frecuencia fundamental de la senal T=1; % Periodo de la senal t=0:.001:T-0.001; %Intervalo en un periodo x=2*cos(wo*t); subplot(311),plot(t,x),grid;title(‚ÄôSe√Īal x(t)‚Äô); xlabel(‚Äôt‚Äô); ylabel(‚Äôx(t)‚Äô); %Senal x1(t): wo1=6*pi; % Frecuencia fundamental de la senal T=1/3; % Periodo de la senal t=0:.001:T-0.001; x1=2*cos(wo1*t); subplot(312),plot(t,x1),grid;title(‚ÄôSe√Īal x1(t)‚Äô); xlabel(‚Äôt‚Äô); ylabel(‚Äôx(t)‚Äô); %Senal m(t): wo2=2*pi; % Frecuencia fundamental de la senal T=1; % Periodo de la senal t=0:.001:T-0.001; m=2*cos(wo2*t)+2*cos(3*wo2*t); subplot(313),plot(t,m),grid;title(‚ÄôSe√Īal m(t)‚Äô); xlabel(‚Äôt‚Äô);ylabel(‚Äôm(t)‚Äô);6. b) Ya que x(t),‚ÄÖx1(t) y m(t) son se√Īales coseno, √©stas se pueden expresar de forma exponencial y obtener los coeficientes de forma directa, esto es
Para la se√Īal x(t), en donde ŌČ0‚ÄÖ=‚ÄÖ2ŌÄ, se tiene:
y los coeficientes espectrales son
Para la se√Īal x1(t)‚ÄÖ=‚ÄÖ2cos(6ŌÄt), en donde ŌČ0‚ÄÖ=‚ÄÖ6ŌÄ, se tiene:
Para la se√Īal m(t)‚ÄÖ=‚ÄÖx(t)‚ÄÖ+‚ÄÖx1(t)‚ÄÖ=‚ÄÖ2cos(ŌČ0 t)‚ÄÖ+‚ÄÖ2cos(3 ŌČ0 t), en donde ŌČ0‚ÄÖ=‚ÄÖ2ŌÄ, se tiene:
6. c) Para obtener los coeficientes de la serie exponencial de Fourier de la se√Īales x(t), x1(t) y m(t) se utilizan las funciones fft() y fftshift(), a partir de los cuales se obtiene el diagrama espectral de cada una de las se√Īales. Ya que los coeficientes son reales se grafica s√≥lo la magnitud de los coeficientes.%senal x(t) wo=2*pi; T=1; t=0:0.001:T-0.001; x=2*cos(wo*t); %Grafica del espectro de x(t) ak=(1/length(t))*fft(x); %calculo de los coeficientes ak ak1=fftshift(ak); %calculo de los coeficientes ak con k=0 centrada k1=(length(ak1)/2)+1; k1=-10:10; subplot(311), stem(k1,ak1(((((length(t)/2)+1))-10):((length(t)/2)+1)+10), ‚ÄôLineWidth‚Äô,2); grid;title(‚ÄôEspectro x(t)‚Äô);xlabel(‚Äôk‚Äô);ylabel(‚Äôak‚Äô);% coeficientes ak axis([-10 10 -.25 1.25]) %senal x1(t) wo1=6*pi; T1=1/3; t=0:.001:T1-0.001; x1=2*cos(wo1*t); %Grafica del espectro de x1(t) ak=(1/length(t))*fft(x1); ak1=fftshift(ak); k1=(length(ak1)/2)+1; k1=-10:10; subplot(312), stem(k1,ak1(((((length(t)/2)+1))-10):((length(t)/2)+1)+10), ‚ÄôLineWidth‚Äô,2); grid;title(‚ÄôEspectro x(t)‚Äô);xlabel(‚Äôk‚Äô);ylabel(‚Äôak‚Äô);% coeficientes ak axis([-10 10 -.25 1.25]) %senal m(t) wo2=2*pi; T2=1; t=0:.001:T2-0.001; m=2*cos(wo*t)+2*cos(wo1*t); %Grafica del espectro de m(t) ak=(1/length(t))*fft(m); ak1=fftshift(ak); k1=(length(ak1)/2)+1; k1=-10:10; subplot(313), stem(k1,ak1(((((length(t)/2)+1))-10):((length(t)/2)+1)+10), ‚ÄôLineWidth‚Äô,2); grid;title(‚ÄôEspectro x(t)‚Äô);xlabel(‚Äôk‚Äô);ylabel(‚Äôak‚Äô);% coeficientes ak axis([-10 10 -.25 1.25])6. d) Para filtrar las se√Īales y recuperarlas, es decir, para obtener y(t)‚ÄÖ=‚ÄÖx(t) y y1(t)‚ÄÖ=‚ÄÖx1(t) se utilizan dos distintos filtros Butterwoth con la funci√≥n butter(), cuya se√Īal de entrada es m(t).
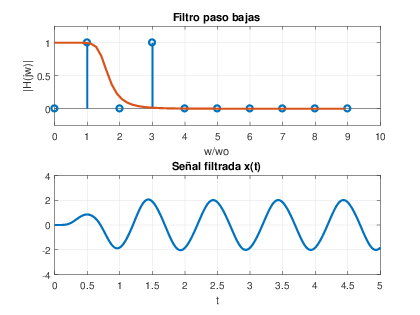
Para y(t)‚ÄÖ=‚ÄÖx(t) se aplica un filtro paso bajas con frecuencia de corte ŌČc‚ÄÖ=‚ÄÖ1.5‚ÄÖŌČ0.
La respuesta en frecuencia del filtro, las componentes espectrales y la salida del filtro se presentan en la figura 5.8.
En la primera gr√°fica se presenta la magnitud de la respuesta en frecuencia del filtro paso bajas (en rojo) y las componentes espectrales de la se√Īal x(t) (en azul). Se observa que el filtro claramente deja pasar la primera componente, k‚ÄÖ=‚ÄÖ1, y atenua pr√°cticamente la segunda componente, k‚ÄÖ=‚ÄÖ2.
En la segunda gr√°fica se presenta la se√Īal x(t) ya filtrada. Se observa el periodo transitorio y la salida permanente en la que se identifica su amplitud y frecuencia, la cual corresponde a x(t).
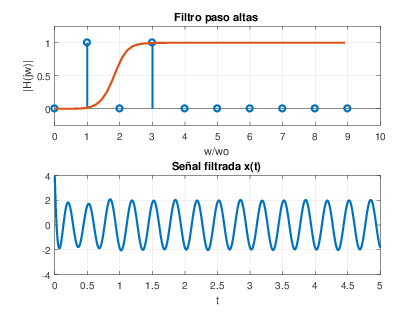
%Senal m(t): wo2=2*pi; T=1; t=0:.001:T-0.001; m=2*cos(wo2*t)+2*cos(3*wo2*t); %Filtro 1 para obtener y(t)=x(t) [b, a] = butter(6,1.5*wo2,‚Äôs‚Äô); %Filtro Paso bajas [H, w] = freqs(b,a); subplot(211),plot(w,abs(H),‚Äôlinewidth‚Äô,2);grid; title(‚ÄôFiltro paso bajas‚Äô);xlabel(‚Äôw‚Äô);ylabel(‚Äô|H(jw)|‚Äô) t=0:.001:5*T-0.001; m=2*cos(wo2*t)+2*cos(3*wo2*t); y=lsim(b,a,m,t); subplot(212),plot(t,y,‚Äôlinewidth‚Äô,2); grid title(‚ÄôSe√Īal filtrada x(t)‚Äô);xlabel(‚Äôt‚Äô);Para el segundo filtrado y1(t)‚ÄÖ=‚ÄÖx1(t) se aplica un filtro paso altas con frecuencia de corte ŌČc‚ÄÖ=‚ÄÖ2‚ÄÖŌČ0.
De nuevo, en la figura 5.9 se observa la respuesta en frecuencia del filtro paso altas y la se√Īal x1(t) recuperada, en la que se identifica su amplitud y frecuencia.
%Senal m(t): wo2=2*pi; T=1; t=0:.001:T-0.001; m=2*cos(wo2*t)+2*cos(3*wo2*t); %Filtro 2 para obtener y1(t)=x1(t) [b, a] = butter(6,2*wo2,‚Äôhigh‚Äô,‚Äôs‚Äô); %Filtro Paso altas [H, w] = freqs(b,a); subplot(211),plot(w,abs(H),‚Äôlinewidth‚Äô,2);grid; title(‚ÄôFiltro paso altas‚Äô);xlabel(‚Äôw‚Äô);ylabel(‚Äô|H(jw)|‚Äô) t=0:.001:3*T-0.001; m=2*cos(wo2*t)+2*cos(3*wo2*t); y=lsim(b,a,m,t); subplot(212),plot(t,y,‚Äôlinewidth‚Äô,2); grid title(‚ÄôSe√Īal recuperada x1(t)‚Äô);xlabel(‚Äôt‚Äô); -
En esta aplicaci√≥n se continua con el concepto de filtrado. Se presenta c√≥mo generar dos se√Īales y como filtrarlas. En este ejercicio se integran los conocimientos de se√Īales, de sistemas y el comportamiento en el dominio de la frecuencia, el cual tiene gran importancia para obtener la respuesta del sistema en el dominio del tiempo.
Se consideran dos se√Īales x(t) y x1(t), una de alta y otra de baja frecuencia respectivamente, que al sumarlas se forma la se√Īal m(t) que simula una se√Īal con interferencia. Se consideran sistemas, A y B, que funcionan como filtros cuya se√Īal de entrada es m(t) y se pretende obtener en las respectivas salidas, separar las dos se√Īales y(t)‚ÄÖ=‚ÄÖx(t) y y1(t)‚ÄÖ=‚ÄÖx1(t) para eliminar la interferencia, tal como se muestra en el diagrama de bloques:- Graficar x(t),‚ÄÖx1(t) y m(t).
- Obtener los coeficientes de la serie de Fourier de las se√Īales x(t),‚ÄÖx1(t) y m(t).
- Graficar el espectro de x(t), x1(t) y m(t).
- Seleccionar y aplicar los filtros Butterwoth apropiados de manera que y(t)‚ÄÖ=‚ÄÖx(t) y y1(t)‚ÄÖ=‚ÄÖx1(t).
Solución
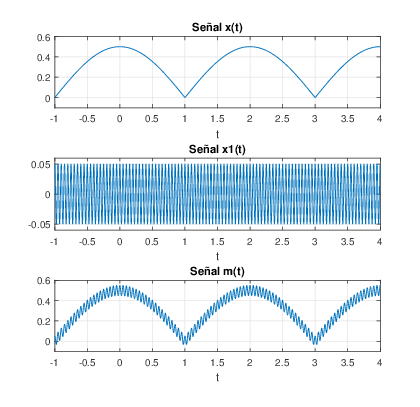
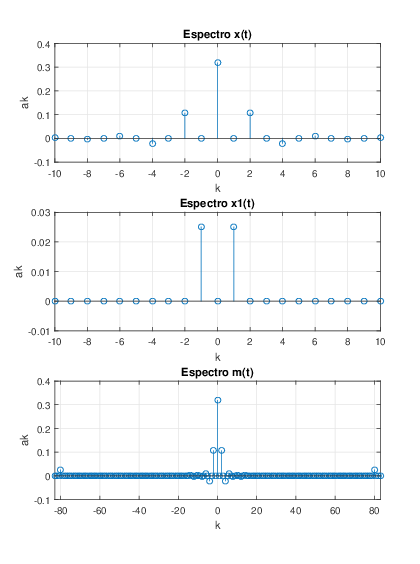
2. a) La gr√°fica de cada una de las se√Īales x(t),‚ÄÖx1(t) y m(t) est=-1:0.001:4-0.001; x=abs((1/2)*cos((pi/2)*t)); x1=(1/20)*cos(40*pi*t); m=x+x1; subplot(311),plot(t,x), title(‚ÄôSe√Īal x(t)‚Äô); xlabel(‚Äôt‚Äô); axis([-1 4 -.1 .6]);grid subplot(312),plot(t,x1),title(‚ÄôSe√Īal x1(t)‚Äô); xlabel(‚Äôt‚Äô); axis([-1 4 -.06 .06]);grid subplot(313),plot(t,m),title(‚ÄôSe√Īal m(t)‚Äô); xlabel(‚Äôt‚Äô); axis([-1 4 -.1 .6]);grid2. b)Coeficientes de x(t)Los coeficientes espectrales se determinan mediante la Ecuaci√≥n de An√°lisis:
los cuales se utilizan para aproximar a la se√Īal a trav√©s de la Ecuaci√≥n de S√≠ntesis de Fourier:
Resolviendo numéricamente la integral definida en un periodo se obtienea0 = 0.3183
a‚ÄÖ‚ąí‚ÄÖ1*‚ÄÖ=‚ÄÖa1‚ÄÖ=‚ÄÖ0
a‚ÄÖ‚ąí‚ÄÖ2*‚ÄÖ=‚ÄÖa2‚ÄÖ=‚ÄÖ0.1061
a‚ÄÖ‚ąí‚ÄÖ3*‚ÄÖ=‚ÄÖa3‚ÄÖ=‚ÄÖ0
a‚ÄÖ‚ąí‚ÄÖ4*‚ÄÖ=‚ÄÖa4‚ÄÖ=‚ÄÖ‚ÄÖ‚ąí‚ÄÖ0.0212
...
Los coeficientes espectrales de cada de una de las se√Īales tambi√©n se pueden obtener mediante las funciones fft() y fftshift().
Coeficientes de x1(t)
Ya que ŌČ0‚ÄÖ=‚ÄÖ(ŌÄ)/(2) , entonces: , la cual corresponde a la arm√≥nica 80, quedando los coeficientes a partir de la Ec. 5.8:
2. c) La gr√°fica la magnitud de los coeficientes de ak con respecto a k se presenta en la figura 5.12. Se observa que en los coeficientes de la se√Īal m(t) aparecen en los extremos los de x1(t) .
%senal x(t) wo=2*pi; T=4; t=0:0.001:T-0.001; x=abs((1/2)*cos((pi/2)*t)); %Grafica del espectro de x(t) ak=(1/length(t))*fft(x); %calculo de los coeficientes ak ak1=fftshift(ak); %calculo de los coeficientes ak con k=0 centrada k1=(length(ak1)/2)+1; k1=-10:10; subplot(311), stem(k1,ak1(((((length(t)/2)+1))-10):((length(t)/2)+1)+10)); grid;title(’Espectro x(t)’); % coeficientes ak xlabel(’k’);ylabel(’ak’); %senal x1(t) wo1=80*pi; T=1/20; t=0:.001:T-0.001; x1=(1/20)*cos(40*pi*t); %Grafica del espectro de x1(t) ak=(1/length(t))*fft(x1); ak1=fftshift(ak); %k1=(length(ak1)/2)+1; k1=-10:10; subplot(312), stem(k1,real(ak1(((((length(t)/2)+1))-10):((length(t)/2)+1)+10))); grid;title(’Espectro x1(t)’);xlabel(’k’);ylabel(’ak’);%coeficientes ak %senal m(t) wo=pi/2; T=4; t=0:.001:T-0.001; m=abs((1/2)*cos((pi/2)*t))+(1/20)*cos(40*pi*t); %Grafica del espectro de m(t) ak=(1/length(t))*fft(m); ak1=fftshift(ak); k1=(length(ak1)/2)+1; k1=-85:85; subplot(313),... stem(k1,real(ak1(((((length(t)/2)+1))-85):((length(t)/2)+1)+85))); grid;title(’Espectro m(t)’);xlabel(’k’);ylabel(’ak’);% coeficientes ak axis([-83 83 -.1 .4])
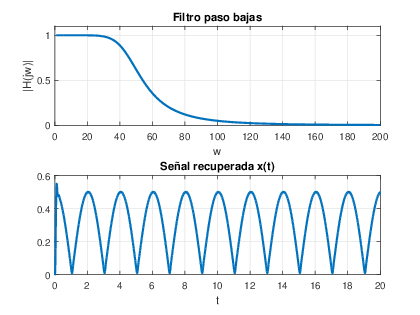
2. d) La se√Īal m(t) es la suma de la se√Īal de baja frecuencia y la de alta frecuencia. Para filtrar las se√Īales, es decir, y(t)‚ÄÖ=‚ÄÖx(t) se aplica un filtro paso bajas de cuarto orden con frecuencia de corte ŌČc‚ÄÖ=‚ÄÖ3‚ÄÖŌČ0 para recuperar x(t). Para la se√Īal de alta frecuencia se selecciona un filtro paso alta de cuarto orden con frecuencia de corte ŌČc‚ÄÖ=‚ÄÖ20‚ÄÖŌČ0
Se presenta la respuesta en frecuencia del filtro y la se√Īal correspondiente se√Īal filtrada.A partir de las figuras 5.13 y 5.14 se observan las se√Īales a la salida del filtro utilizando la funci√≥n lsim().%Senal m(t): wo=pi/2; T=4; t=0:.001:T-0.001; m=abs((1/2)*cos((pi/2)*t))+(1/20)*cos(40*pi*t); %Filtro 1 para obtener y(t)=x(t) [b, a] = butter(4,30*wo,‚Äôs‚Äô); %Filtro Paso bajas [H, w] = freqs(b,a); subplot(211),plot(w,abs(H),‚Äôlinewidth‚Äô,2);grid; title(‚ÄôFiltro paso bajas‚Äô);xlabel(‚Äôw‚Äô);ylabel(‚Äô|H(jw)|‚Äô) axis([0 200 0 1.1]) t=0:.001:5*T-0.001; m=abs((1/2)*cos((pi/2)*t))+(1/20)*cos(40*pi*t); y=lsim(b,a,m,t); subplot(212),plot(t,y,‚Äôlinewidth‚Äô,2); grid title(‚ÄôSe√Īal recuperada x(t)‚Äô);xlabel(‚Äôt‚Äô); figure %Filtro 2 para obtener y1(t)=x1(t) [b, a] = butter(4,20*wo,‚Äôhigh‚Äô,‚Äôs‚Äô); %Filtro Paso altas [H, w] = freqs(b,a); subplot(211),plot(w,abs(H),‚Äôlinewidth‚Äô,2);grid; title(‚ÄôFiltro paso altas‚Äô);xlabel(‚Äôw‚Äô);ylabel(‚Äô|H(jw)|‚Äô) axis([0 200 0 1.1]) t=0:.001:1*T-0.001; m=2*cos(wo2*t)+2*cos(3*wo2*t); y=lsim(b,a,m,t); subplot(212),plot(t,y,‚Äôlinewidth‚Äô,2); grid title(‚ÄôSe√Īal recuperada x1(t)‚Äô);xlabel(‚Äôt‚Äô);FiltroPasoBajas:y(t)‚ÄÖ=‚ÄÖx(t) Para que la se√Īal de salida y(t) sea igual a x(t), es necesario aplicar un filtrado. Y ya que lo que se desea eliminar es la arm√≥nica n√ļmero 80, la cual es de frecuencia alta, es necesario utilizar un sistema que sea un filtro Paso Bajas, en el cual la frecuencia de corte debe estar entre y .
Para generar un sistema filtro en MatLab se utiliza la función butter(), la cual toma como parámetros el orden del sistema, la frecuencia de corte, el tipo de filtro y el dominio en el que dará la respuesta, tal como se muestra:
t=0:0.001:4-0.001; x=abs((1/2)*cos((pi/2)*t)); x1=(1/20)*cos(40*pi*t); m=x+x1; [b,a]=butter(2,8*pi,’s’); b = 0 0 631.6547 a = 1.0000 35.5431 631.6547Esta función proporciona los valores de los vectores a y b que son los coeficientes de la Función de Transferencia.
La función freqs() genera la respuesta del sistema en el dominio de la frecuencia tomando como parámetros los coeficientes a y b obtenidos anteriormente.
[H w]=freqs(b,a); subplot(321),plot(w,abs(H));grid;title(’Paso baja’) subplot(323),plot(w,angle(H)*180/pi);grid subplot(325),y1=lsim(b,a,m,t); plot(t,y1);grid
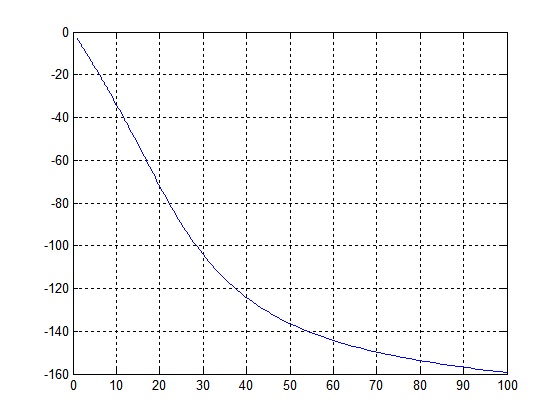
Y graficando el valor absoluto de H y sus √°ngulos se obtiene:
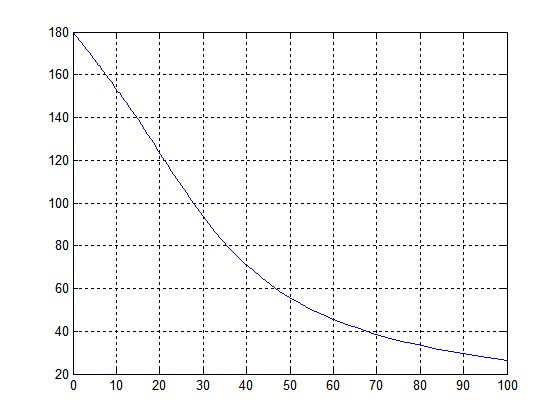
Se observa que este sistema en la arm√≥nica 80 la aten√ļa en 0.1. Esto es:Los √°ngulos de H(jŌČ) muestran el desfasamiento que puede provocar el sistema en la se√Īal a la salida del filtro.
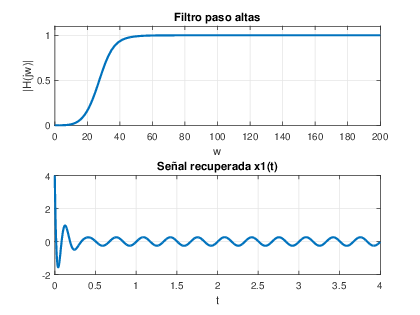
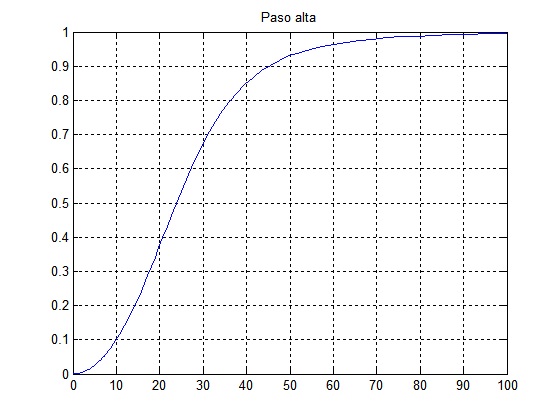
Finalmente, la se√Īal de respuesta de este sistema obtenida al darle como entrada a m(t) es:Con esto se observa que este sistema reduce en un factor considerable la interferencia que ten√≠a la se√Īal de entrada aproximandose a la se√Īal x(t). Aunque considerando que hay un leve retraso de la se√Īal en la gr√°fica y que al inicio se presenta un intervalo transitorio de la se√Īal.Filtro Paso Altas: y1(t)=x1(t)Para que la se√Īal de salida y1(t) sea igual a x1(t), es necesario aplicar la se√Īal a un sistema que dejar pasar la arm√≥nica n√ļmero 80, la cual es de frecuencia alta, por lo que es necesario utilizar un filtro Paso Altas, en el cual la frecuencia de corte debe estar entre y .
[b,a]=butter(2,10*pi,’High’,’s’) b = 1 0 0 a = 1.0000 44.4288 986.9604Código tomado del archivo proyecto c.mLa Función de Transferencia de este filtro es:Obteniendo la respuesta en frecuencia de este sistema tenemos:
[H w]=freqs(b,a); subplot(322),plot(w,abs(H));grid;title(‚ÄôPaso alta‚Äô) subplot(324),plot(w,angle(H)*180/pi);grid subplot(326),y1=lsim(b,a,m,t); plot(t,y1);gridGraficando el valor absoluto de H y sus √°ngulos obtenemos:En este sistema observamos que en la primera arm√≥nica se aten√ļa en aproximadamente 0.001 y que la arm√≥nica 80 la aten√ļa en 0.99. Esto es:Finalmente, la se√Īal de respuesta de este sistema obtenida al aplicar como entrada m(t) es:Se observa que este sistema es un filtro cuya se√Īal de respuesta es una buena aproximaci√≥n a la funci√≥n x1(t). Aunque sigue presentando el mismo problema, ya que al inicio de la gr√°fica hay un transitorio considerable y a lo largo de la se√Īal se observan ligeras deformaciones de la se√Īal.
-
En esta aplicaci√≥n se generan y grafican dos se√Īales x(t) y x1(t), se obtiene la resultante de la suma de las mismas m(t). Se obtiene la gr√°fica de los espectros de cada una y por √ļltimo se seleccionan los filtros adecuados para separar las dos se√Īales y(t) y y1(t). Previamente se obtienen los coeficientes espectrales de cada se√Īal de forma anal√≠tica.
Considere el diagrama de bloques de la figura 5.21 y las se√Īales x(t) y x1(t). La se√Īal x(t) es peri√≥dica con T‚ÄÖ=‚ÄÖ2 como se muestra en la figura 5.22.
- Obtener la expresión de x(t) y graficar x(t), x1(t) y m(t).
- Obtener los coeficientes de la serie de Fourier deblas se√Īales x(t),‚ÄÖx1(t) y m(t).
- Graficar el espectro de x(t), x1(t) y m(t).
- Seleccionar y aplicar los filtros Butterwoth apropiados de manera que y(t)‚ÄÖ=‚ÄÖx(t) y y1(t)‚ÄÖ=‚ÄÖx1(t).
-
Preguntas de investigación y reflexión.
- En este ejercicio, los filtros seleccionados fueron de orden 6, pruebe el mismo ejercicio con filtros de orden 2 y 4 e identifique que diferencias existen.
- Compare la salida de ambos filtros con las correspondientes se√Īales de entrada e identifique que diferencia existe.
- Para los filtros de segundo orden, obtenidos con la función butter(), exprese la función de transferencia, el modelo en el dominio del tiempo y la expresión de la respuesta en frecuencia de cada filtro.
- Para cada uno de los filtros de segundo orden, grafique la respuesta en frecuencia en magnitud y √°ngulo.
- En las gr√°ficas de la respuesta en frecuencia de los filtros de orden 6, se ha presentado s√≥lo la magnitud y no se ha incluido el √°ngulo de fase. ¬ŅComo afecta el √°ngulo de fase del filtro en la se√Īal filtrada?
Soluci√≥n La se√Īal periodica x(t) se muestra en la figura 5.23, cuyo periodo es T‚ÄÖ=‚ÄÖ2, la cual se define como
en donde T es el periodo y m es entero constante para la repetici√≥n de la se√Īal. Si m‚ÄÖ=‚ÄÖ0, la expresi√≥n de x(t) queda como Tambi√©n se puede definir en segmentos, en un periodo, para este caso se tomar√° el intervalo de ‚ÄÖ‚ąí‚ÄÖ1‚Äւȧ‚ÄÖt‚Äւȧ‚ÄÖ1 quedando como
La periodo y la frecuencia de la se√Īal x(t) son
Para obtener los coeficientes espectrales se utiliza la ecuación de Análisis
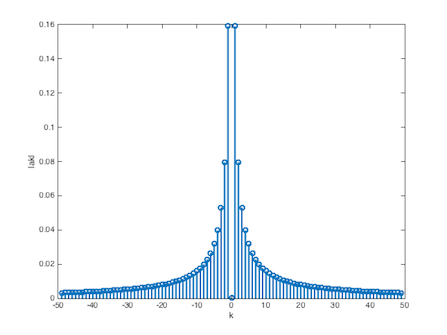
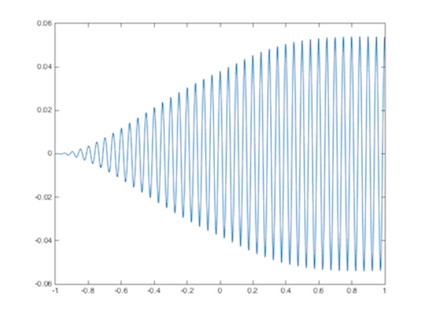
Para la funci√≥n definida por la Ec. 5.15 y sustituyendo en Ec. 5.16:Resolviendo primeramente las integrales indefinidasSustituyendo, evaluando y simplificando se obtiene el valor de las integrales definidas comoFinalmente quedaEvaluando paraque al observar la figura 5.23 se identifica directamente que el √°rea de la se√Īal en un periodo es cero, por lo que el valor promedio tambi√©n es cero. O bien se obtiene a0, el valor promedio de la se√Īal a partir deEvaluando para k‚ÄÖ=‚ÄÖ1 donde y|a1|‚ÄÖ=‚ÄÖ0.15915y as√≠ sucesivamente, obteniendok|ak|0010.159120.079530.0530540.0397850.03183La se√Īal x1(t) se presenta en la figura 5.24 es un coseno de alta frecuencia que altera x(t) cuando se suman las se√Īales, interpret√°ndose como interferencia.
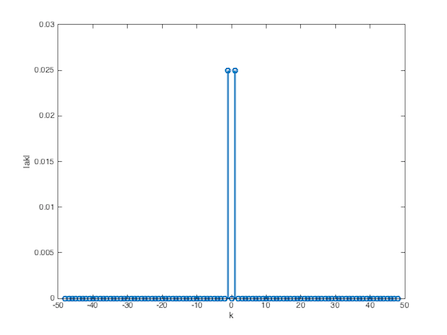
Para obtener los coeficientes de la se√Īal se tienex1 = (1/20)*cos(40*pi*t); figure(8); plot (t,x1);
Los coeficientes se obtienen de manera directa
La se√Īal m(t), se muestra en la figura 5.25.
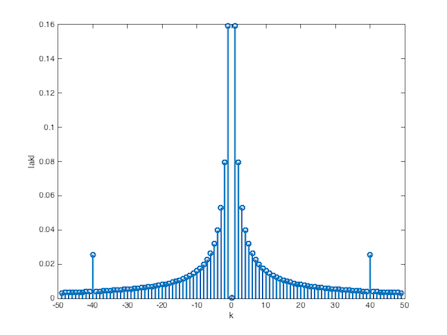
m = x + x1; figure(2); plot (t,m);Para obtener los coeficientes de la se√Īal m(t), ck, se aplica la propiedad de linealidad, sumando los coeficientes de la se√Īal x(t) con los de x1(t). El periodo y la frecuencia de la se√Īal son T‚ÄÖ=‚ÄÖ2 y ŌČ0‚ÄÖ=‚ÄÖŌÄ, obteniendock‚ÄÖ=‚ÄÖak‚ÄÖ+‚ÄÖbkc0‚ÄÖ=‚ÄÖa0‚ÄÖ+‚ÄÖb0‚ÄÖ=‚ÄÖ0c1‚ÄÖ=‚ÄÖa1‚ÄÖ+‚ÄÖb1‚ÄÖ=‚ÄÖj 0.1591c2‚ÄÖ=‚ÄÖa2‚ÄÖ+‚ÄÖb2‚ÄÖ=‚ÄÖj 0.0795...c40‚ÄÖ=‚ÄÖa40‚ÄÖ+‚ÄÖb40‚ÄÖ‚Čą‚ÄÖ0.025Verificaci√≥n con Matlab
Se presentan las gr√°ficas obtenidas mediante el uso de funciones de Matlab.
El espectro de x(t) se muestra en la figura 5.26 se calcula con el mismo periodo que se us√≥ en las gr√°ficas anteriores dado que este mismo era el periodo de un diente de sierra.ak=(1/length(t))*fft(x); %calculo de los coeficientes ak ak1=fftshift(ak); %calculo de los coeficientes ak con k=0 centrada k1=(length(ak1)/2)+1; k1=-10:10; ak(1:5) stem(k1,abs(ak1(((((length(t)/2)+1))-10):((length(t)/2)+1)+10)),‚ÄôLineWidth‚Äô,2); grid;title(‚ÄôCoeficientes {a_k} de x(t)‚Äô);xlabel(‚Äôk‚Äô);ylabel(‚Äôak‚Äô);Para el coseno se utiliza un vector diferente que es t1 porque es una se√Īal con periodo distinto.t1=0:0.001:(1/20)-0.001; x2 = (1/20)*cos(40*pi*t1); ak = (1/length(t1))*fft(x2); ak = ak(1:50) ak = [ak(49:-1:1) ak(2:49)]; k = (-48:48); figure(4); stem(k,abs(ak),‚ÄôLineWidth‚Äô,2),xlabel(‚Äôk‚Äô),ylabel(‚Äô|ak|‚Äô);
A continuacion se muestra el espectro de las se√Īales sumadas:ak = (1/length(t))*fft(m); ak = ak(1:50); ak = [ak(50:-1:1) ak(2:50)]; k = (-49:49); figure(5); stem(k,abs(ak),‚ÄôLineWidth‚Äô,2),xlabel(‚Äôk‚Äô),ylabel(‚Äô|ak|‚Äô);
Filtrado de Se√Īales
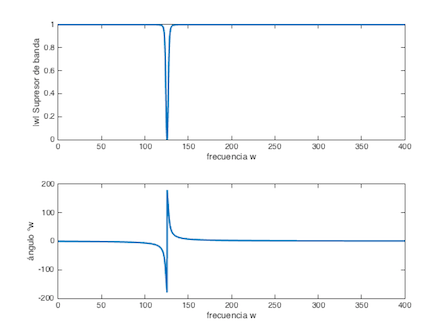
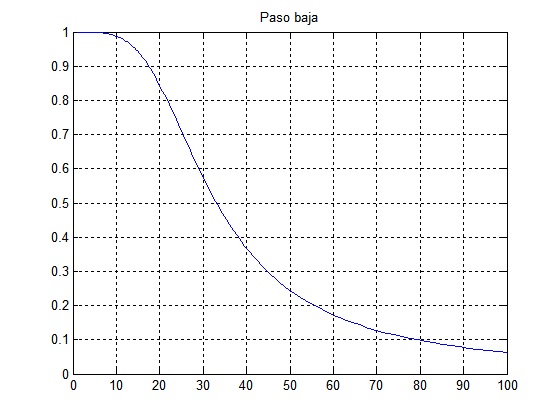
Los filtros seleccionados fueron utilizados de acuerdo con la supresi√≥n o paso de la frecuencia kŌČ0 asociada a los valores 40*ŌÄ equivalente a 125.6.
Las gr√°ficas de las se√Īales ya filtradas y un acercamiento a cada una de ellas que demuestra el uso del filtro definido y la supresi√≥n o paso de la frecuencia con los valores antes mencionados.El uso de un filtro supresor de banda es necesario para obtener la se√Īal x(t).wo = pi; wn = [(39.3205)*wo (40.6725)*wo]; [b a] = butter(2,wn,‚Äôstop‚Äô,‚Äôs‚Äô); w=0:0.01:400; [h w] = freqs(b,a,w); figure(6); subplot(211),plot(w,abs(h),‚ÄôLineWidth‚Äô,2),xlabel(‚Äôfrecuencia w‚Äô),ylabel(‚Äô|w| Supresor de banda‚Äô); subplot(212),plot(w,angle(h)*180/pi,‚ÄôLineWidth‚Äô,2),xlabel(‚Äôfrecuencia w‚Äô),ylabel(‚Äôangulo ‚Äôw‚Äô); y = lsim(b,a,m,t); figure(10); subplot(111),plot (t,y);Un filtro paso banda para obtener el ruido (x1(t)):wo = pi; wn = [(39.3205)*wo (40.6725)*wo]; [b a] = butter(2,wn,‚Äôs‚Äô); w=0:0.01:400; [h w] = freqs(b,a,w); figure(7); subplot(211),plot(w,abs(h),‚ÄôLineWidth‚Äô,2),xlabel(‚Äôfrecuencia w‚Äô),ylabel(‚Äô|w| Supresor de banda‚Äô); subplot(212),plot(w,angle(h)*180/pi,‚ÄôLineWidth‚Äô,2),xlabel(‚Äôfrecuencia w‚Äô),ylabel(‚Äôangulo ‚Äôw‚Äô); y = lsim(b,a,m,t); figure(9); subplot(111),plot (t,y);Finalmente se presenta el resultado de las se√Īales filtradas y por lo tanto, separadas: x(t) para la Figura 9 y x1(t) para la Figura 10.
Serie de Fourier de TC nivel avanzado:
fm=500; tm=1/fm ‚Äč t=0:tm:5; % Se√Īal sinusoidal de periodo 2, que el tiempo de inicio es cero To=2; fo=1/To; ‚Äč p=sin(2*pi*fo*t); plot(t,p) % para tener medio periodo se genera una senoidal que dure un segundo % se multiplica la se√Īal senoidal por un pulso formado por una resta de % escalones p=(us(t)-us(t-1)).*p; ‚Äč %la multiplocaci√≥n de ambas funciones da como resultante un l√≥bulo de la senoidal, %mismo que inicia en t=0 y termina en t=1 % con lo que se obtiene la onda buscada ‚Äč % se busca obtener una rampa de pendiente unitaria que inicie en t=2 y % termine en t=3, observe que la expresi√≥n que describe a la rampa es % t-2 evaluada a partir de 2 ‚Äč q=rs(t-2)-2*rs(t-3)+rs(t-4); ‚Äč % finalmente se suman las funciones calculadas y se obtiene la gr√°fica ‚Äč pqr=p+q; ‚Äč plot(t,pqr) axis([0 5 -0.5 1.5]) ‚Äč
a) el semiciclo senoidal cuya expresión es
‚Äč
t=[0:tm:5];
comp=30;
y=zeros(1,length(t));
for n=1:comp
%componentespara la se√Īal triangular
an=(2*((5*(-5*cos((4*n*pi)/5.) + 5*cos((6*n*pi)/5.) + 2*n*pi*sin((6*n*pi)/5.)))/...
(4.*power(n,2)*power(pi,2)) - (5*(-5*cos((6*n*pi)/5.) + 5*cos((8*n*pi)/5.) + 2*n*pi*sin((6*n*pi)/5.)))/...
(4.*power(n,2)*power(pi,2))))/5.;
bn=(2*((-5*(2*n*pi*cos((6*n*pi)/5.) + 5*sin((4*n*pi)/5.) - 5*sin((6*n*pi)/5.)))/...
(4.*power(n,2)*power(pi,2)) + (5*(2*n*pi*cos((6*n*pi)/5.) + 5*sin((6*n*pi)/5.) - 5*sin((8*n*pi)/5.)))/...
(4.*power(n,2)*power(pi,2))))/5.;
%componentes para el lobulo positivo de la senoidal
an_s=-((cos((5*pi+2*pi*n)/5))/(5*pi+2*pi*n))-((cos((5*pi-2*pi*n)/5))/(5*pi-2*pi*n)) +(1/(5*pi+2*pi*n))...
+(1/(5*pi-2*pi*n));
bn_s=((sin((5*pi-2*pi*n)/5))/(5*pi+2*pi*n))-((sin((5*pi+2*pi*n)/5))/(5*pi-2*pi*n));
f2=(an_s)*cos(2*pi*n*t/5)+(bn_s)*sin(2*pi*n*t/5);
f1=(an)*cos(2*pi*n*t/5)+(bn)*sin(2*pi*n*t/5);
y=y+f2+f1;
plot(t,y)
pause(0.1)
end
y=(1/5)+y;
plot(t,y)
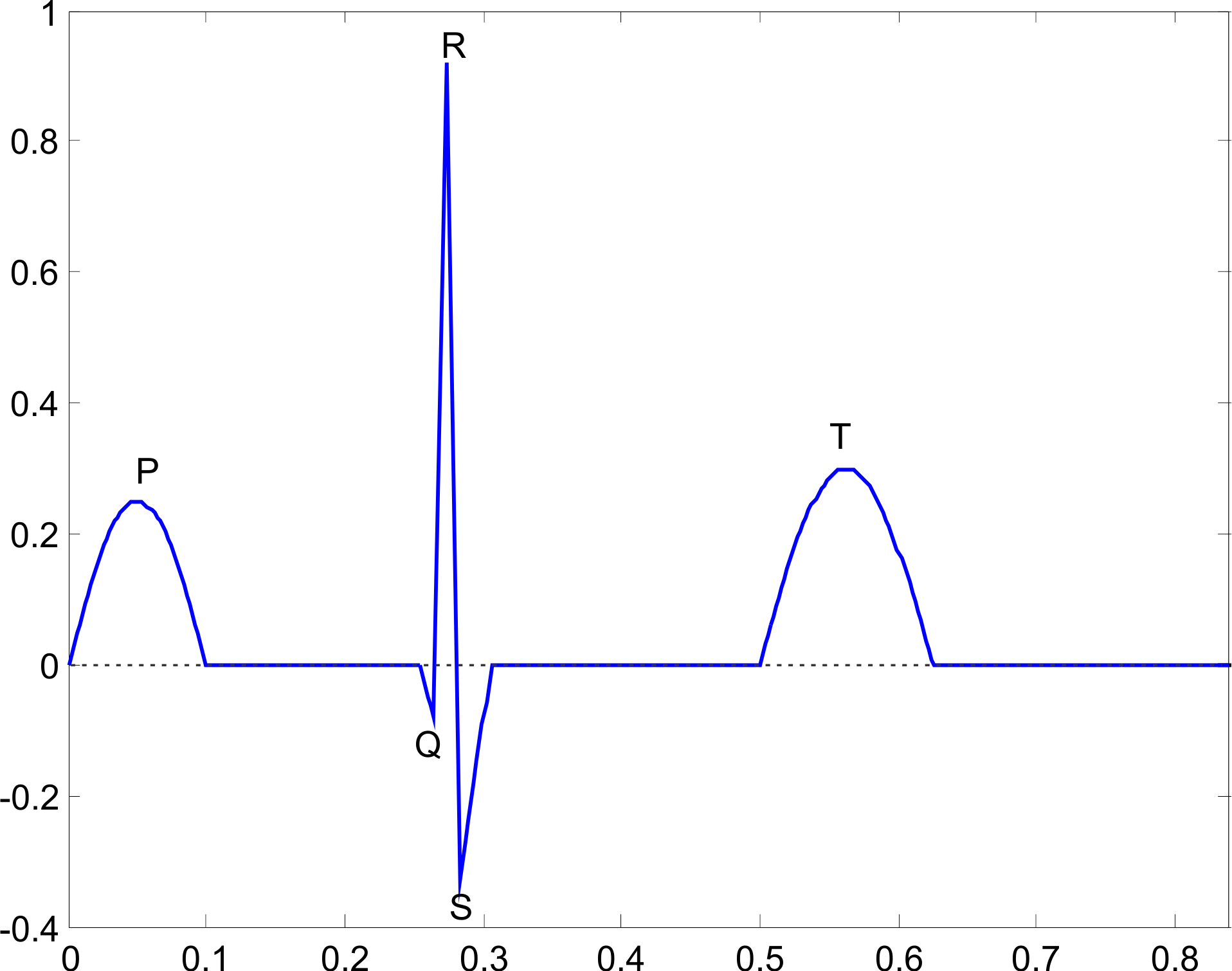
| Onda | Amplitud [mv] | Duración [s] | Limites (t) | ||||
| P | 0.25 | 0.1 | 0 | - | 0.1 | ||
| PQ | 0.156 | 0.1 | - | 0.256 | |||
| Q | -0.08 | 0.01 | 0.256 | - | 0.266 | ||
| QR | 1 | 0.01 | 0.266 | - | 0.276 | ||
| RS | 0.01 | 0.276 | - | 0.286 | |||
| S | -0.33 | 0.02 | 0.286 | - | 0.308 | ||
| ST | 0.194 | 0.308 | - | 0.502 | |||
| T | 0.3 | 0.125 | 0.502 | - | 0.627 | ||
| TP | 0.236 | 0.627 | - | 0.84 | |||
Análisis de Fourier en TD:
En esta secci√≥n de Fourier TD se aplican los conceptos en se√Īales peri√≥dicas de TC para realizar un an√°lisis en el dominio de la frecuencia.
Bajo este antecedente se introduce el concepto de filtrado de se√Īales en TD.
En análisis anterior sirve de base para realizar un sistema de detección de tonos de marcado bajo el esquema de multifrecuencia de doble tono (DTMF).
Selecciona la dificultad en las caritas de la izquierda.
Análisis de Fourier en TD: nivel principiante:
Mediante las funciones butter() y freqz(), obtenga el siguiente filtro:
Obtenga la expresi√≥n de la respuesta en frecuencia de un filtro digital Butterworth paso baja de segundo orden, con una frecuencia de corte ŌÄ‚ÄÖ‚ĀĄ‚ÄÖ10 y grafique la respuesta en frecuencia en amplitud. Verifique la frecuencia de corte.
Análisis de Fourier en TD: nivel intermedio:
En esta actividad la se√Īal x[n] se compone de 4 cosenos. Se utilizaran los filtros para separar cada una de las se√Īales como se indica en la Figura 6.5.
- Obtenga el espectro de la se√Īal x[n] y graf√≠quelo.
- Mediante la funci√≥n butter(), seleccione el filtro m√°s adecuado con el que se pueda separar cada una de las se√Īales.
- Utilice la función freqz(), grafique la respuesta del filtro y verifique si se ha recuperado adecuadamente la componente de x[n].
Análisis de Fourier en TD: nivel avanzado:
En tel√©fonos con marcaci√≥n por Tono, al presionar cada bot√≥n se genera un conjunto √ļnico de se√Īales de dos tonos, que se denominan se√Īales de multifrecuencia de doble tono (DTMF), que se procesan para identificar el n√ļmero marcado determinando las dos frecuencias de tonos asociadas. Se utilizan siete frecuencias para codificar los diez d√≠gitos y los dos botones especiales marcados "*"y "#". Las frecuencias de banda baja son 697Hz, 770Hz, 852Hz y 941 Hz. Las restantes tres frecuencias pertenecientes a la banda alta son 1209Hz, 1336Hz, y 1477Hz. La cuarta frecuencia de banda alta de 1633Hz no se usa y se ha asignado para aplicaciones que permitan el uso de cuatro botones para servicios especiales. Las asignaciones de frecuencia utilizadas en el esquema de marcado por Tono se muestran en la Figura 6.6.
-
Genere los tonos correspondientes a cada bot√≥n. Por ejemplo, para el d√≠gito 1 se tiene: d1[n]‚ÄÖ=‚ÄÖsin‚éõ‚éĚ(ŌČ1n)/(őĪ)‚éě‚醂ÄÖ+‚ÄÖsin‚éõ‚éĚ(ŌČ5n)/(őĪ)‚éě‚é†
en donde d1 es la se√Īal para el tono del bot√≥n No. 1 y őĪ es la frecuencia de muestreo de 8192 Hz. - Genere los vectores d0 a d9 para representar los 10 d√≠gitos con una longitud n de 0‚Äւȧ‚ÄÖn‚Äւȧ‚ÄÖ9999. Escuche la se√Īal con sound(). Por ejemplo sound(d1,8192).
-
La funci√≥n fft() calcula N muestras de la DTFT de una se√Īal de longitud finita a las frecuencias ŌČk‚ÄÖ=‚ÄÖ(2ŌÄk)/(N)para 0‚Äւȧ‚ÄÖk‚Äւȧ‚ÄÖN‚ÄÖ‚ąí‚ÄÖ1.
Por ejemplo, D0 = fft (d0,2048) calcula 2048 muestras correspondientes al espectro del dígito d0.
Grafique la respuesta en frecuencia para cada dígito. - Defina un vector ’spa’ de 500 muestras con la función zeros, que permitirá dejar un espacio entre tono y tono.
-
Defina un vector que contenga un n√ļmero de tel√©fono:
tel = [do spa d1 spa d2 spa ...]
Escuche el tono con sound(). - Analice y realice el algoritmo para separar las frecuencias y detectar el No. marcado.
- Obtenga la gráfica del espectro de cada dígito e identifique las frecuencias de cada componente.
- Obtenga la gr√°fica de la respuesta en frecuencia del filtro paso bajas.
- Obtenga la gr√°fica de la respuesta en frecuencia del filtro paso altas.
- Obtenga las gr√°ficas de la respuesta en frecuencia de los filtros paso banda.
- Identifique en cada caso las frecuencias de corte.






.jpg)
.jpg)